TOPIC 1: APPLICATION OF VECTORS
Scalar and Vector Quantities
Difference between Scalar and Vector Quantities
Distinguish between scalar and vector quantities
Scalar Quantities
These are physical quantities which have magnitude only. Examples of scalar quantities include mass, length, time, area, volume, density, distance, speed, electric current and specific heat capacity.
Vector Quantities
These are physical quantities which have both magnitude and direction. Examples of vector quantities include displacement, velocity, acceleration, force, pressure, retardation, and momentum.
Addition of Vectors Using Graphical Method
Add vectors using graphical method
Scalar physical quantities have magnitude only. Thus, they can be added, multiplied, divided, or subtracted from each other.
Example 1
If you add a volume of 40cm3 of water to a volume of 60cm3 of water, then you will get 100cm3 of water.
Vectors can be added, subtracted or multiplied conveniently with the help of a diagram.
Vectors Representation
A vector quantity can be represented on paper by a direct line segment.

- The length of the line segment represents the magnitude of a vector.
- The arrow head at the end represents the direction.
Methods of Vector Addition
There are two methods that are used to sum up two vectors:
- Triangle method
- Parallelogram method.
Triangle Method
A step-by-step method for applying the head-to-tail method to determine the sum of two or more vectors is given below.
1.Choose a scale and indicate it on a sheet of paper. The best choice of scale is one that will result in a diagram that is as large as possible, yet fits on the sheet of paper.
2.Pick a starting location and draw the first vectorto scalein the indicated direction. Label the magnitude and direction of the scale on the diagram (e.g., SCALE: 1 cm = 20 m).
3.Starting from where the head of the first vector ends, draw the second vectorto scalein the indicated direction. Label the magnitude and direction of this vector on the diagram.
4.Draw the resultant from the tail of the first vector to the head of the last vector. Label this vector as Resultantor simplyR.
5. Using a ruler, measure the length of the resultant and determine its magnitude by converting to real units using the scale (4.4 cm x 20 m/1 cm = 88 m).
6.Measure the direction of the resultant using the counterclockwise convention.
Resultant vector: This is the vector drawn from the starting point of the first vector to the end point of the second vector which is the sum of two vectors.
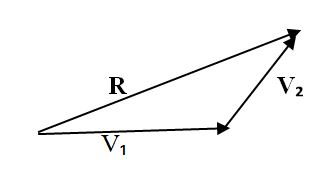
Where:
- Vi - First vector
- V2 - Second vector
- R - Resultant vector
Example 2
Suppose a man walks starting from point A, a distance of 20m due North, and then 15m due East. Find his new position from A.
Solution
Use scale
1CM Represents 5m
Thus
20m due to North Indicates 4 cm
15m due to East Indicates 3cm.
Demonstration
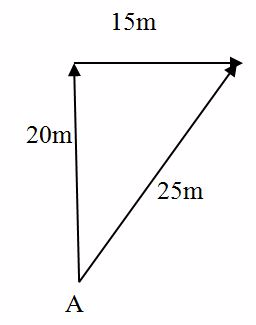
The position of D is represented by Vector AD of magnitude 25M or 5CM at angle of 36051”
Since
- Tan Q = (Opposite /Adjacent)
- Tan Q = 3cm /4cm
- Q = Tan -1 (3/4)
- Q = Tan -1(0.75)
- Q = 35º51”
The Resultant displacement is 25m ad direction Q = 36º51”
The Triangle and Parallelogram Laws of Forces
State the triangle and parallelogram laws of forces
Triangle Law of Forces
Triangle Law of Forces states that “If three forces are in equilibrium and two of the forces are represented in magnitude and direction by two sides of a triangle, then the third side of the triangle represents the third force called resultant force.”
Example 3
A block is pulled by a force of 4 N acting North wards and another force 3N acting North-East. Find resultant of these two forces.
Demonstration
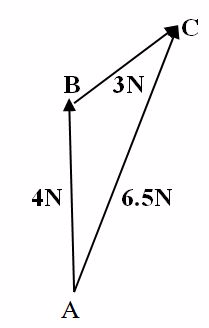
Scale
1Cm Represents 1N
Draw a line AB of 4cm to the North. Then, starting from B, the top vectorofAB, draw a line BC of 3 CM at 45oEast of North.
Join the line AC and measure the length (AC = 6.5 cm) which represents 6.5N. Hence, AC is the Resultant force of two forces 3N and 4N.
Parallelogram Method
In this method, the two Vectors are drawn (usually to scale) with a common starting point , If the lines representing the two vectors are made to be sides of s parallelogram, then the sum of the two vectors will be the diagonal of the parallelogram starting from the common point.
The Parallelogram Law states that “If two vectors are represented by the two sides given and the inclined angle between them, then the resultant of the two vectors will be represented by the diagonal from their common point of parallelogram formed by the two vectors”.
Example 4
Two forces AB and AD of magnitude 40N and 60N respectively, are pulling a body on a horizontal table. If the two forces make an angle of 30o between them find the resultant force on the body.
Solutiuon
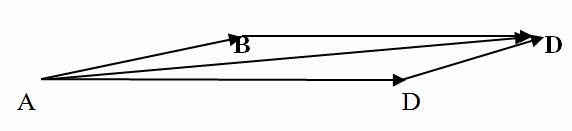
Choose a scale.
1cm represents10N
Draw a line AB of 4cm
Draw a line AD of 6cm.
Make an angle of 30o between AB and AD. Complete the parallelogram ABCD using the two sides AB and include angle 30O.
Draw the lineAC with a length of9.7 cm, which is equivalent to 97 N.
The lineAC of the parallelogram ABCD represents the resultant force of AB and AD in magnitude and direction.
Example 5
Two ropes, one 3m long and the other and 6m long, are tied to the ceiling and their free ends are pulled by a force of 100N. Find the tension in each rope if they make an angle of 30obetween them.
Solution
1cm represents 1N
Thus
3cm = represent 3m
6cm = represents 6m
Demonstration
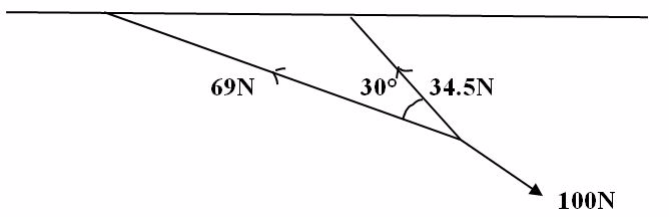
By using parallelogram method
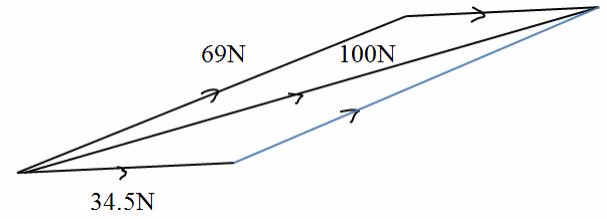
Tension, determined by parallelogram method, the length of diagonal using scale is 8.7 cm, which represents 100N force.
Thus.
Tension in 3m rope = 3 X 100 / 8.7 = 34.5N
Tension in 6m rope = 6 x 100 / 8.7 =69N
Tension force in 3m rope is 34.5N and in 6m rope is 69N.
Note: Equilibrant forcesare those that act on a body at rest and counteract the force pushing or pulling the body in the opposite direction.
Relative Motion
The Concept of Relative Motion
Explain the concept of relative motion
Relative motion is the motion of the body relative to the moving observer.
The Relative Velocity of two Bodies
Calculate the relative velocity of two bodies
Relative velocity (Vr) is the velocity relative to the moving observer.
CASE 1: If a bus in overtaking another a passenger in the slower bus sees the overtaking bus as moving with a very small velocity.
CASE 2: If the passenger was in a stationary bus, then the velocity of the overtaking bus would appear to be greater.
CASE 3: If the observer is not stationary, then to find the velocity of a body B relative to body A add velocity of B to A.
Example 6
If velocity of body B is VB and that of body A is VA, then the velocity of B with respect to A , the relative velocity VBA is Given by:
VBA = VB + (-VA)
That is
VBA = VB – VA
NOTE:The relative velocity can be obtained Graphically by applying the Triangle or parallelogram method.
For same direction
VrBA = VB - (+VA)
= VB – VA ___________________ (I)
For different direction
VrBA = VB – (-VA)
VrBA = VB + VA _______________________ (II)
Example 7
A man is swimming at 20 m/s across a river which is flowing at 10 m/s. Find the resultant velocity of the man and his course if the man attempted to swim perpendicular to the water current.
Solution
Scale
1cmrepresents 2m/s
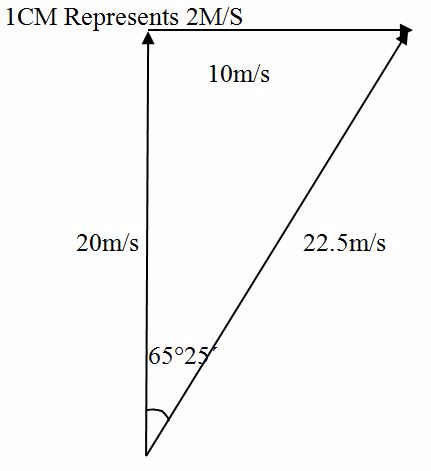
- The length of AC is 11.25 cm which is 22.5 m/s making a angle of 65º25’ with the water current.
- The diagonal AC represent (in magnitude and direction) the resultant velocity of the man.
The Concept of Relative Motion in Daily Life
Apply the concept of relative motion in daily life
Knowledge of relative motion is applied in many areas. In the Doppler effect, the received frequency depends on the relative velocity between the source and receiver. Friction force is determined by the relative motion between the surfaces in contact. Relative motions of the planets around the Sun cause the outer planets to appear as if they are moving backwards relative to stars in universe.
Resolution of Vectors
The Concept of Components of a Vector
Explain the concept of components of a vector
Is the Splits or separates single vector into two vectors (component vectors) which when compounded, provides the resolved vector.
Resolved vector is asingle vector which can be split up into component vectors.
Component vectorsare vectors obtained after spliting up or dividing a single vector.
Resolution of a Vector into two Perpendicular Components
Resolve a vector into two perpendicular components
Components of a vector are divided into two parts:
- Horizontal component
- Vertical component
Take angle OAC
Case 1
SinQ = FX/F
Thus
FX = F SinQ
Horizontal component, FX = FSinQ
Case 2
Cos Q = Fy/F
Thus:
Fy = FCosQ
Vertical component: Fy = FCosQ
Resolution of Vectors in Solving Problems
Apply resolution of vectors in solving problems
Example 8
Find the horizontal and vertical components of a force of 10N acting at 300 to the vertical.
Solution
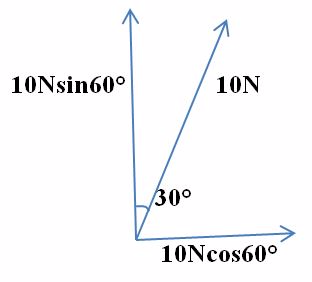
FX = FCOS 60º
Since
Cos 60º /F =(FX)
FX = F CoS60º _________________(1)
FX = 10NCos 60º
Fy = ?
Sinq = Fy
Fy =F SinQ __________________________ (ii)
Fy= 10N Sin 60º
TOPIC 2: FRICTION
Concept of Friction
The Concept of Friction
Explain the concept for friction
Friction is the force which opposes (resists) motion of the body for example: If a block of wood is placed on a table it remains at rest Unless it is acted upon by an external force.
The applied force must exceed the maximum friction force between the block of wood and the table if the block is to be moved along the table.
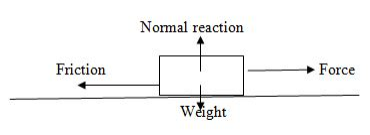
Friction force between two surface in contact exists only when there is relative motion between the two contacting surface.
The friction between two surfaces exists because of the nature of the surface of the bodies in contact. (Strictly speaking all surfaces are rough because they are made up of peaks and valleys)
Demonstration
The peak and valleys on the surfaces of bodies may be due to a random arrangement of coarse particles, for example the surface of a gridding stones.
Smooth surfaces exert almost no friction. What happens when two objects are pushed?
When one body is pushed against another, the peaks of one surface have to rise up over the peaks of the other surface. Hence opposition to motion or friction occurs the force acting to restore the bodies to their original position.
The Advantages and Disadvantages of Friction in Daily Life
Realize the advantages and disadvantages of friction in daily life
Advantages of Friction
Thefriction force has several advantages which includes the following:
- It helps in walking process (because friction force stop us from slipping over).
- It helps cars to move onroads easily due to friction between car tyres and road (makesa car stay on road) NOTE: Most car tyres have deep dreads to increase friction between the tyres and the road surface.
- it helps in car braking system. Brakes rely on friction between the brake drum or pads and the wheels. In a bicycle, there are brake pads which clamp onto the wheel to slow it down.
Disadvantages of friction
Frictional force has several dis-advantages which includes the following:
- Cause machinery to heat up and can cause wear and tear.
- Cause machinery to be less efficient.
- Cause machinery to produce noise.
Methods of Reducing Friction
Describe methods of reducing friction
Thedifferent methods ofreducing friction between surfaces includes the following:
- Polishing:Polishing the surface, reduces the irregularities and hence, reduces friction.
- Lubrication:It provides a layer of the lubricant on which the bodies can easily slide.
- Use of ball-bearing or roller bearing:Roller bearing help to convert sliding friction into a milder form-rolling friction. Rolling friction is lesser than sliding friction.
- Streamlining:Fast cars, boats, planes etc., have a streamlined body. This is to allow air (or water in the case of boats) to easily flow by, without offering much resistance. Flying birds have streamlined bodies.
- Use of correct combination of surfaces in contact:Use of alloys on moving and sliding parts reduces friction because alloys have a low coefficient of friction.
Roller
- It is a simple cylinder on which a body to be pulled RESTS.
- It is used to eliminates sliding friction.
- Conveyor belts use metal rollers.
Wheels
- These arerollers that are fixed to a moving body, held in place by cylinders or axles which are threaded in their centers. Example; a trailer towed by vehicle.
- Wheels are used to eliminate sliding friction.
- They are used to reduce friction (the friction between surfaces can be reduced by smoothing and polishing the surfaces in contact).
- In order to make surfaces slippery, a lubricant such as oil or graphite is used. Oil and Grease are commonly used invehicles and machines to reduce friction between moving parts. In engines, differential air is also an effective lubricant in machine.
Types of Friction
Types of Friction
Identify types of friction
There are three main types of friction in daily life which include the following:
- Static friction: an opposing forcebetween two solid objectsat rest.In simple words, when there is no relative motion between two solid objects in contact with each other, we describe the frictional force between them asstatic.
- Limiting friction: numerically equal to the minimum external force required to make a body just move over another.
- Dynamic friction: numerically equal to the force of opposition when a body is moving over the rough surface.
Limiting Friction
Determine limiting friction
Limiting friction is equal to the minimum external force required to make a body just move over one another. Is the maximum possible value of static friction. It is the frictional force that must be overcome before an object starts moving. The coefficient of friction will be the same for all masses. The limiting frictional forces is independent of applied force but depends on nature of surface.
Example 1
A block of mass 20 kg is pulled along a horizontal surface. If the coefficient of friction is 0.4, what force is acting on the block?
Solution
Force = coefficient of friction ×mass × acceleration due to gravity
F = 0.420×10 = 80N.
Laws of Friction
Laws of Friction
State laws of friction
The five laws of friction
- When an object is moving, the friction is proportional and perpendicular to the normal force (N).
- Friction is independent of the area of contact.
- The coefficient of static friction is slightly greater than the coefficient of kinetic friction.
- Within rather large limits, kinetic friction is independent of velocity.
- Friction depends upon the nature of the surfaces in contact.
The Coefficient of Friction
Determine the coefficient of friction
Coefficient of friction is the ratio of the frictional force that acts between two objectsin contact to the normal reaction, R.
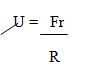
Types of Coefficient of friction
There are three main types of coefficient of frictions which includes the following:
Coefficient of static friction is the ratio of the static friction to the normal reaction.
Us =Frs/R
Coefficient of dynamic friction US
Is the ratio of the dynamic friction to the normal reaction that acts onthe body.
Ud = Frd/R
Laws of Friction in Solving Problems
Apply laws of friction in solving problems
Demonstration to determine coefficient of dynamic friction.
Method of calculation
The coefficient of dynamic friction U is
U = Frictional force, Fr/Normal Reaction, R
U= Fr/R_______________________________ ( I)
By Resolving forces we get
Fr = W SinQ __________________________(II)
R= W CosQ ________________________(III)
Put Eqn (iii) ad (ii) into eqn (i)
U =W SinQ/Wc osQ
U =W SinQ/WCosQ
But SinQ/CosQ=TanQ
U=TanQ
Thus
TanQ = (AB/CB) FROM Angle ABC
But
U = TanQ
u = (ab/cb)
Example 2
Find the static friction between a block of wood of mass 10kg and the table on which it rests. A minimum force of 50N is required to make the block just move on the table top.
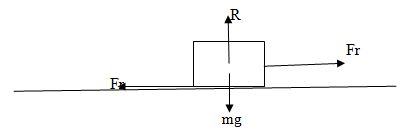
Solution
Limiting Friction, Fr = 50N
Normal Reaction, r =(10 X 10 ) = 100N
Coefficient of static friction; Us
Us = (Fr/ R)
Us = (50/100)
Us = 0.5
Therefore,coefficient of static friction, Us = 0.5
Example 3
A mass is placed on an Inclined plane such that it moves at a constant speed when tapped tightly. If the angle the plane makes with the horizontal is 30º. Find the coefficient of dynamic friction.
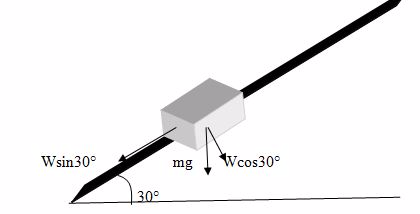
The Coefficient of friction U =Fr/R
Fr = WSinQ/R = WCosQ
At Equilibrium
U =WSinQ/wCosQ
U = (W/W) (SinQ/CosQ)
But (SinQ/CosQ) = TanQ
U = Tan 30º
U = 0.56
Coefficient of friction, U = 0.56






