FORM THREE PHYSICS STUDY NOTES TOPIC TOPIC 3: LIGHT & TOPIC 4: OPTICAL INSTRUMENT

 TOPIC 3: LIGHT

Light is aform of energy which controls the sense of vision.

Reflection of Light from Curved Mirrors

Difference between Concave and Convex Mirrors

Distinguish between concave and convex mirrors

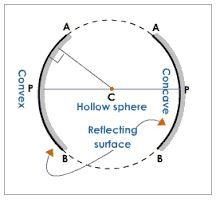
Concave mirror is a spherical mirror whose reflecting surface is curved inwards. A Good example is the driving mirror of a car.

Convex mirror is a spherical mirror whose reflective surface is curved outwards. A good example of a convex mirror is a shaving mirror.

General demonstrations of convex and concave mirrors (curved mirrors:

The Terms Principle, Axis, Pole, Principle Focus and Radius of Curvature as Applied to Curved Mirrors

Explain the terms principle, axis, pole, principle focus and radius of curvature as applied to curved mirrors

Terms used in studying curved mirrors

• Centre of curvature (C):the centre of the sphere of which a mirror is a part of.
• Radius of curvature (R): the radius of sphere of which a mirror is a part of.
• Pole (P): the central point of the reflecting surface of spherical mirror (curved or convex mirror).

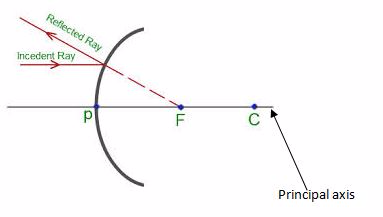
• Principal axis:the straight line joining the centre of curvature (C) and the pole (P).
• Principal focus (F):the point o the principal axis where light rays tend to intersect. This point is between centre of curvature and the pole.
• Principal axis:the straight line joining the centre of curvature (C) and the pole (P).
• Principal focus (F):the point on the principal axis where light rays tend to intersect. This point is between centre of curvature and the pole.

The Images Formed by a Curved Mirror

Locate the images formed by a curved mirror

Case (1)

When a beam of light parallel and very close to the principal axis, CL, is reflected from a concave mirror, it converges to a point, F, on the principal axis called the principal focus.

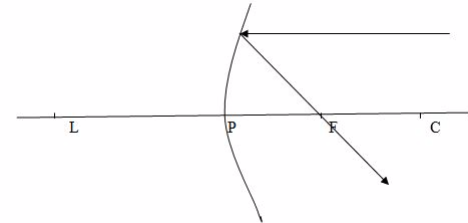
Case 2

When a ray passes through the principal focus, F, it is reflected parallel to the principal axis.

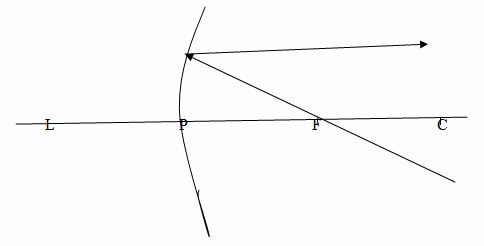
Case 3

When a ray passes through the centre of curvature, C, which therefore strikes the mirror at normal incidence, it is reflected back along its original path.

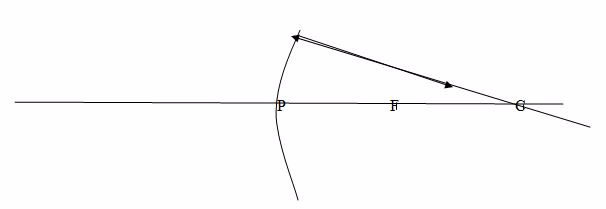
Note: Concave mirrors have a real focus because light passes through the focus.

The formation of images by concave mirror tends to change as the position of object changes.

Case 1: Image (I) formed by a concave mirror when the object is beyond C.

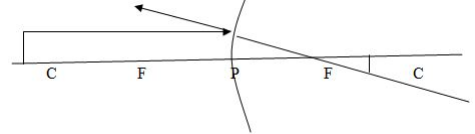
Properties of images formed:

1. The image is between C and F
2. The image is smaller than the object
3. The image is inverted (upside down)
4. The image is real

Case 2: The object is placed at C

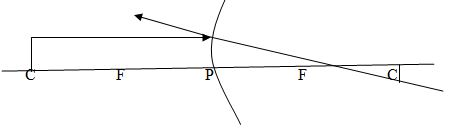
Properties of image

1. The image is formed at C
2. The image has the same size as object
3. The image is inverted (upside down)
4. The image is real.

Case 3: The object is placed between C and F

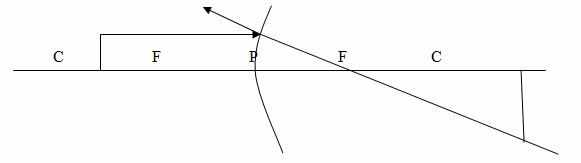
Properties of image formed

1. The image is real
2. The image is large than object
3. The image is formed beyond C
4. The image is inverted (upside down)
5. The image is real
6. The image is large than object
7. The image is formed beyond
8. The image is inverted (upside down)

Case 4:The object is placed at F

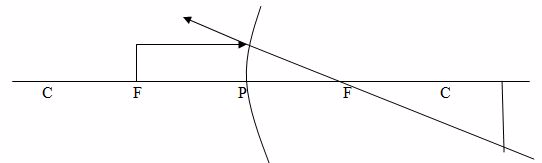
Properties of image:

1. The image is formed at infinity (x)
2. The image is formed beyond C
3. The image is large than object
4. The image is Real

Case 5:The object is placed between F and P.

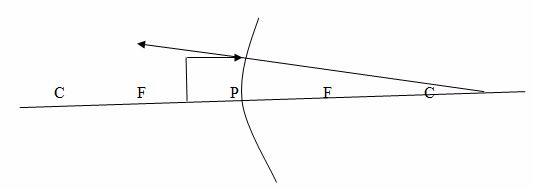
Properties of image formed:

1. The image is virtual
2. The images is upright
3. The image is formed behind the mirror
4. The image is large than the object

Formation of images in a convex mirror:

Obviously,there isonly one kind of image formed when an object is placed at any position.

Properties of image formed by convex mirror:

1. the image is virtual
2. the image is upright
3. The image is smaller than object (diminished)
4. The image is formed behind the mirror.

Example 1

An object 2cm long is erected 8cm infront of a concave mirror of radius of curvature 10cm. By using a scale drawing, determine the position, size and nature of image formed.

Data given

• Height of object, Ho = 2cm
• Object distance, U= 8cm
• Radius of curvature, r = 10cm
• Focal length,f =8cm
• Choose suitable scale.
• Say 1cm represents 5cm

From this scale then

• Height of object, Ho = 2cm
• Object distance, U= 2cm
• Focal length, F = 2.5cm

Thus,

Image distance, V = X

Image Height, H1=Y

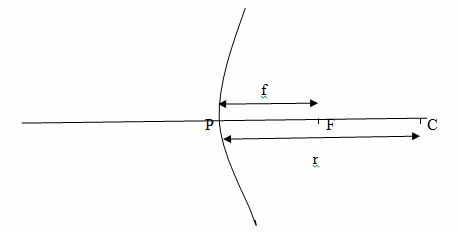
The Focal Length of a Concave Mirror

Determine practically the focal length of a concave mirror

Focal length (f) is the distance between the principal focus and the pole.

Convex and Concave Mirrors in Daily Life

Use Convex and concave mirrors in daily life

Curved mirrors are used as:

1. Driving mirrors
2. Shaving mirrors
3. Reflectors

Question Time 1

Why is convex mirror used as driving mirror?

The convex mirror is used as driving mirror because it provides the wider field of view.

Question Time 2

Why concave mirror used as shaving mirror?

Concave mirrors are used as shaving mirrors because they form an enlarged image when held close up.

Refraction of Light

The Concept of Refraction of Light

Explain the concept of refraction of light

Refraction of light refers tothe bending of light as it passes through two different medium because the speed of light tends to change when travelling from one medium to another.

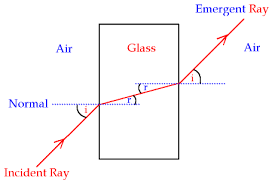
Figure showing refraction of light as it passes from air to glass.

The Angle of Incidence and Angle of Refraction

Measure the angle of incidence and angle of refraction

The angle of incidence (i)is the angle between the incident ray of light and the normal at the point of incidence.

The angle of Refraction (r)is the angle between the refracted ray and the normal at the point of incidence.

The Laws of Refraction

State the laws of refraction

First law of refraction

The First Law of refraction states that "the incident ray, the refracted ray and the normal at the point of incident are located in the same plane.”

Second law of refraction

Second Law of refraction states that “when a light ray passes from one medium into another medium, the angle of incidence (i) and corresponding angle of refraction( r) are such that the ratio of sine of the angle of incidence to the sine of the angle of refraction (sini/sinr) is a constant value called the refractive index."

Note: The Second Law of Refraction is called Snell's Law in honour of a Dutch scientist named Snell (1591 – 1626) who first described it.

The Refraction Index of a Material

Determine the refraction index of a material

Refractive index (n) is the ratio of the sine of the angle of incidence to the sine of the angle of refraction.

n = Sini/Sinr OR

Refractive index (n) is the ratio of the velocity of light in air to the velocity of light in glass.

n = Velocity of light in air (Va)/Velocity of light in glass (Vg)

Or

Refractive index, n is the constant number which expresses how many times or to what extent a light ray bends when passing through different medium.

Absolute refractive index (na) is the refractive index between vacuum or air and any other medium.

The refractive indices between air and some common media is given below:

Medium	Refractive index (n)
Diamond	2.417
Ethanol	1.360
Glass (Crown)	1.520
Quartz	1.553
Water (at 20ºC0	1.333
Air (at stp)	1.00029

Example 2

The refractive index for light passing from air to water is equal to 1.333 find the refractive index for light travelling from water to air.

Data given:

Refractive index anw of air to water = 1.333

Required: To find refractive index from water to air

Since

anw = 1.333

wna = (1/anw)

= (i/1.333)

: wna = 0.75

Real and Apparent Depth

Real depthis the actual height measured without taking account any refraction of light

Apparent depth is the virtual height measured when viewed by observer.

The Concept of Critical Angle and Total Internal Reflection of Light

Explain the concept of critical angle and total internal reflection of light

Critical angle

Critical angleis the angle of incidence (i) for which the angle of refraction (r) is equal to 90º . It is obtained when light rays moves from a dense medium to a less dense medium.

For refractive index

n=Sini/sinr

But i= Critical angle, C

r = 90º

Thus n= sinC/sin 90º

n=SinC/1

n = Sin C

c= Sin -1 (n)

Total Internal Refraction

This occurs when a light ray from a less dense medium is reflected into the denser medium at the boundary separating the two media.

Conditions for total internal reflection to occur include the following:

1. Light must be travelling from a more dense to less dense medium.
2. Light must incident at the boundary at an angle greater than the critical angle (C).

Optical fibres

These are very thin tubes of plastic or glass and because they are so thin they can bend without breaking, so they can carry light around the corners.

Uses of optical fibres

• Used in telecommunications to carry telephone calls over vast distance, without loss of intensity and without interference.
• Used in endoscope to view inside a patient body for example inside stomach. Light is carried into the stomach through a bunch of fibres and is reflected into small camera, which then displays a picture on a screen.

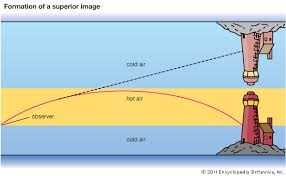
The Occurance of Mirage

Explain the occurrence of mirage

This is the phenomenon inwhich an object appears to be at an incorrect position due to the bending of light rays from the object.

Mirages occur during hot days.

Refraction of Light by Rectangular Prism

The Passage of Light through a Triangular Prism

Trace the passage of light through a triangular prism

Deviation of light in a prism is the changing in direction of the incident ray when it enters/hits a triangular glass prism.

Where i

is the angle of incidence

s is the angle of deviation

The minimum angle of deviation ( qm)

In order to determine the minimum angle deviating (Qm) then we must set triangular Glass prism as follows.

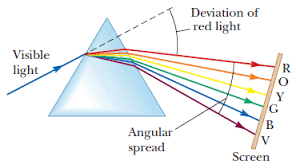
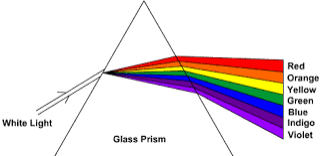
The Dispersion of White Light

Demonstrate the dispersion of white light

Dispersion of light is the splitting up of light beam (white light) into its seven components of colour by a prism.

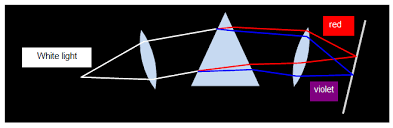
Spectrum is the patch or band of colours which comprise / constitute seven component of white light.

Pure section is the patch or band of colours in which the colours are clearly separated.

In order to produce pure spectrum then we must use two converging lenses (convex lenses).

When colours of spectrum are combined, they form white light.

In order to combine colours of the spectrum, weneed two triangular glass prisms and one lens.

Impure spectrum:the band/patch of colours which overlap and are not seen clearly.

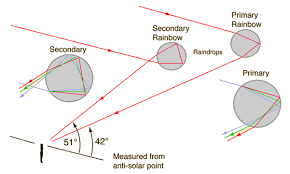
The rainbow:a bow-shaped spectrum of seven colours of white light formed when white light undergoes dispersion within the rain drops because water is denser than air, so has a large refractive index.

Activity 1

A rainbow can be demonstrated as follows:

Spray some water into the air in a direction opposite to that of the sun.

Look at the water shower while you face away from the sun. You will see the colour of the spectrum of white light in the falling drops of water. The spectrum so formed hasthe shape like a bow. So it is called rainbow.

There are two main types of rainbow:

1. Primary rainbow
2. Secondary rainbow

Primary rainbow

This is formed when light undergoes one or single total internal reflection in the water droplets. In this type of the rainbow the violet colour is on the inside of the bow while the red colour is on the outside.

The Angles of Deviation and Minimum Deviation

Determine the angles of deviation and minimum deviation

Finding the refractive index (n) of glass by using the deviation of light in a prism:

Refracting angle of prism is A

Snell’s law

S in i/Sin r = N

Sin i= n sin r

Sin e’ = nsin i

From Geometry of figure

I = A- r

The total angle of deviation (s) is the angle between the direction orf the incident ray and the emergent ray.

Again from the Geometry Q is given by:

S= i+r’- A

When the deviation is a minimum (Sm) the passage of light through the prism will be symmetrical so:

I = r ‘and r = I’

This means that;

A + Smin = 2i = 2r’

Therefore;

Refractive index, n = Sin (A + Smin)/2

Sin (A/2)

Where

A = Apex angle ( angle of prism)

Smin – The angle of minimum deviation

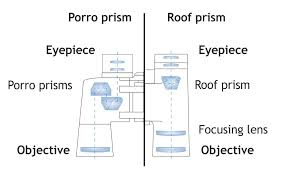
A Simple Prism Binocular

Construct a simple prism binocular

Simple prism binocular

Colours of Light

The Component of White Light

Explain the component of white light

There are two types of colour of light

1. Primary colour of light
2. Secondary colour of light

Primary colour of light

These are basic (fundamental ) Colour of light to which the eye is most sensitive.Primary Colour of light Include the following

1. Red
2. Green
3. Blue

Secondary colours of light

These are colour of light obtained after mixing primary colours of light

Colour mixing by Addition

This is the process of combining primary colours of light without loss any colour to form secondary colours of light.

	Primary color	Secondary color
	Red + Blue	Magenta
	Red + Green	Yellow
	Blue + Green	Cyan

Colours of White Light

Recombine colours of white light

When all white light ( Red , Blue and Green)Combineforms WHITE LIGHT.

Complementary colours of light: These are the colours which produce white light when combined.

• Red + Blue+ Green - White light
• Red + Cyan - White light
• Blue + Yellow - White light
• Green + Magenta - White light

The Appearances of Coloured Object under White Light

Explain the appearances of coloured object under white light

There are two types of coloured paints ( pigments) which Include the following

1. Primary coloured pigment (paints)
2. Secondary coloured pigment (paints)

Primary, Secondary and Complementary Colours of Light

Identify primary, secondary and complementary colours of light

Primary Coloured pigments

These are basic coloured pigments which form secondary coloured pigment when combined.

The primary coloured pigments include:Yellow, Cyan and Magenta

Secondary colour pigments

These are coloured pigments which are formed when two primary colours combine, whichis always accompanied with the removal of other colours.

Difference between Additive and Subtractive Combination of Colours

Distinguish between additive and subtractive combination of colours

Colour Mixing by Substration

Is the process of mixing two primary coloured paints ( pigments) to form secondary colour white.

Example 3

• Magenta + Cyan
• Magenta = ( Blue) + ( Red)
• Cyan = (Blue) + (green)

The colour which is common to Blue will appear while red and green disappear.

Magenta + Cyan = Blue

Example 4

• Magenta + yellow
• Magenta = (Blue) + (Red)
• Yellow = (Green) + (Red)

The colour which is common to both red will appear while blue and green will disappear.

Hence

Magenta + Yellow = Red

Example 5

• Cyan + yellow
• Cyan = (Blue) + (Green)
• Yellow = (Red) + (Green)

The colour which is common to both green will appearwhile Blue and Red will disappear

Hence

Cyan + Yellow = Green

Refraction of Light by Lenses

Difference between Convex and Concave Lenses

Distinguish between convex and concave lenses

A lens is a transparent medium bounded by two surfaces of regular shape. There are two major categories of lenses which include:

The Terms Focal Length, Principle Focus, Principle Axis and Optical Centre as Applied to Lenses

Explain the terms focal length, principle focus, principle axis and optical centre as applied to lenses

Optical center is a geometric center of a lens. Center of curvature is the center of the sphere in which a lens is a part. Principal axis is an imaginary line which passes through the optical center of the lens at right angle to the lens. Principle focus is a point through which all rays traveling close and parallel to the principal axis pass through.

The Focal Length of a Lens

Determine practically the focal length of a lens

Focal length is a distance between between optical centre and the principal focus. It is important to note that the the principal focus is not the halfway between the optical centre and the centre of curvature in lenses as it is in mirrors. The plane through the principal focus which is at right angles with the principal axis is called the focal plane.

Example 6

An object is 2 cm high and placed 24cm from a convex lens. An image formed 72 cm. find the focal length of the lens.

Solution

i/f = 1/u + 1/v

1/f =1/24 + 1/72

1/f = 4/72

f = 18cm.

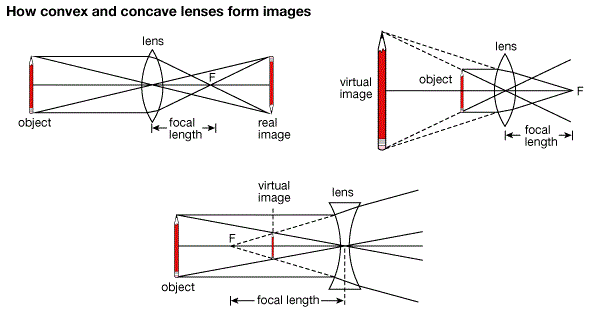
The Immage Formed by a Lens

Locate the image formed by a lens

Rays diagrams are normally used toillustratesthe formation of images by lenses.

1. A ray parallel to the principal axis passes through or appears to diverge from the principal focus after refraction.
2. A ray of light passing through the principal focus of a lens is refracted parallel to the principal axis of the lens.
3. A ray of light through the optical center of the lens continues throughundeviated(Not change direction)

The position, Size and Nature of the Image formed by Lens

Determine the position, size and nature of the image formed by lens

The nature, position and size of the image formed by a lens depends on the position of the object in relation to the type of lens. For example in converging lens when the object is between the lens and principal focus the image will be formed at the same side as the object but further from the lens. It is virtual, erect, and magnified. The image by concave lens is erect, virtual and reduced.

Activity 2

1. Take a convex lens. Find its approximate focal length in a way described in Activity 11.
2. Draw five parallel straight lines, using chalk, on a long Table such that the distance between the successive lines is equal to the focal length of the lens.
3. Place the lens on a lens stand. Place it on the central line such that the optical centre of the lens lies just over the line.
4. The two lines on either side of the lens correspond to F and 2F of the lens respectively. Mark them with appropriate letters such as 2F1, F1, F2and 2F2, respectively.
5. Place a burning candle, far beyond 2F1to the left. Obtain a clear sharp image on a screen on the opposite side of the lens.
6. Note down the nature, position and relative size of the image.
7. Repeat this Activity by placing object just behind 2F1, between F1and 2F1at F1, between F1and O. Note down and tabulate your observations.

The nature, position and relative size of the image formed by convex lens for various positions of the object is summarized in the table below:

Position of the object	Position of the image	Relative size of the image	Nature of the image
At infinity	At focus F2	Highly diminished, point-sized	Real and inverted
Beyond 2F1	Between F2and 2F2	Diminished	Real and inverted
At 2F1	At 2F2	Same size	Real and inverted
Between F1and 2F1	Beyond 2F2	Enlarged	Real and inverted
At focus F1	At infinity	Infinitely large or highly enlarged	Real and inverted
Between focus F1and optical centre O	On the same side of the lens as the object	Enlarged	Virtual and erect

Activity 3

1. Take a concave lens. Place it on a lens stand.
2. Place a burning candle on one side of the lens.
3. Look through the lens from the other side and observe the image. Try to get the image on a screen, if possible. If not, observe the image directly through the lens.
4. Note down the nature, relative size and approximate position of the image.
5. Move the candle away from the lens. Note the change in the size of the image. What happens to the size of the image when the candle is placed too far away from the lens.

Nature, position and relative size of the image formed by a concave lens for various positions of the object

Position of the object	Position of the image	Relative size of the image	Nature of the image
At infinity	At focus F1	Highly diminished, point-sized	Virtual and erect
Between infinity and optical centre O of the lens	Between focus F1and optical centre O	Diminished	Virtual and erect

The Magnification of the Lens Camera

Determine the magnification of the lens camera

As we have a formula for spherical mirrors, we also have formula for spherical lenses. This formula gives the relationship between object distance (u), image-distance (ν) and the focal length (f ). The lens formula is expressed as1/ν - 1/u = 1/f(8)

The lens formula given above is general and is valid in all situations for any spherical lens. Take proper care of the signs of different quantities, while putting numerical values for solving problems relating to lenses.

The magnification produced by a lens, similar to that for spherical mirrors, is defined as the ratio of the height of the image and the height of the object. It is represented by the letter m. If h is the height of the object and h′ is the height of the image given by a lens, then the magnification produced by the lens is given by,m = Height of the Image / Height of the object = h' / h(9)

Magnification produced by a lens is also related to the object-distance u, and the image-distance ν. This relationship is given byMagnification (m ) = h' / h = ν / u(10)

Example 7

A concave lens has focal length of 15 cm. At what distance should the object from the lens be placed so that it forms an image at 10 cm from the lens? Also, find the magnification produced by the lens.

Solution

A concave lens always forms a virtual, erect image on the same side of the object.

Image-distance v = –10 cm;

Focal length f = –15 cm;

Object-distance u = ?

Since, 1 /v - 1 / u = 1 / f

or, 1 / u = 1 / v - 1 / f

1 / u = 1 / -10 - 1 / (-15) = - 1 / 10 + 1 / 15

1 / u = (-3+2) / 30 = 1 / (-30)

or, u = - 30 cm.

Thus, the object-distance is 30 cm.

Magnification m = v/ u

m = -10 cm / -30 cm = 1 / 3 = +0.33

The positive sign shows that the image is erect and virtual. The image is one-third of the size of the object.

The Relationship between Focal Length (f) Object Distance (u) and Image Distance (v) as Applied to Lenses

Determine the relationship between focal length (f) object distance (u) and image distance (v) as applied to Lenses

The lens equation is given as 1/f =1/u + 1/v , if sign convection is used for u, v and f the equation applies to both converging and diverging lenses for all cases of object and image.

Example 8

An object is placed 12 cm from converging lens of focal length 18 cm. Find the position of the image.

Solution

Since the lens is converging f = +18 cm. 1/v = 1/18 -1/12, v = -36.

The image is virtual.

TOPIC 4: OPTICAL INSTRUMENT 

Simple Microscope

The Structure of the Simple Microscope

Describe the structure of the simple microscope

A magnifying glass, an ordinary double convex lens with a short focal length, is a simple microscope. The reading lens and hand lens are instruments of this type. When an object is placed nearer such a lens than its principal focus, i.e., within its focal length, an image is produced that is erect and larger than the original object. The image is also virtual; i.e., it cannot be projected on a screen as can a real image.

The Mode of Action of a Simple Microscope

Describe the mode of action of a simple microscope

The image formed by magnifying glass or simple microscope is virtual and erect object place between principal focus (f) and convex lens.

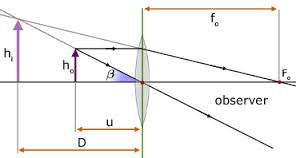
• The normal district vision
• The position of the lens is usually adjusted so that V is about 25cm, which is the shortest distance of distinct vision.

Using the equation of lens (Lens formula).

I/U + I/V = I/F

Adopting the 'real is positive' sign convention we obtain:

V = (-Ve) since the image is virtual.

I/U – I/V = I/F

V= 25 –(Normal district vision)

I/U – I/25 =I/F

I/U = I/F + I/25

(I/U)=-1 (25 + F )

25F

U = 25F/F+25

The above formula shows the means of obtaining the distance of object, U.

Magnication (M) of simple microscope

Magnification is the ratio of the image distance to the object distance.

M = Image distance, V

Object distance, U

Hence

M = v/u …………………..(i)

From V = 25cm (distance of district vision)

From U = 25f/(f+25) ……………………… (ii)

Insert eqn (ii) into (i)

M = V/ (25f/(f+25)

M = 25/(25f/f+25)

M = 25/f + 1

Example 1

A simple microscope with lens of focal length 5cm is used to read division of a scale 0.5mm in size. How large will the division be seen through the simple microscope?

Data given

• Focal length, f = 5cm
• Required to find magnification, M

Soln:

From

M = (25/f + 1)

= (25/5+1)

=(5+1)

= 6

The magnification of lens = 6

Let the size of the object be ho and that of the image be hi. Then:

M = h1/H ……………(i)

H1 = 6h

The Height , h = (0.5mm)

H1 = 6 (0.5mm)

HI = 3mm

Hence, each division will appear to have a size of 3.0mm viewed through the simple microscope.

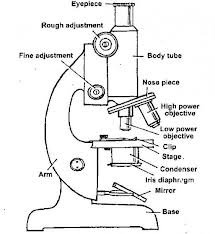
A Simple Microscope

Construct a simple microscope

Parts of simple microscope

Compound Microscope

The Structure of a Compound Microscope

Describe the structure of a compound microscope

A compound microscope is an optical instrument used to produce much greater magnification than that produced by simple microscope. The main features of a compound microscope includes two short-focus convex lenses, the objective lens, and the eyepiece.

Demonstration

The Mode of Action of a Compound Microscope

Describe the mode of action of a compound microscope

The most commonly used microscope for general purposes is the standard compound microscope. It magnifies the size of the object by a complex system of lens arrangement.

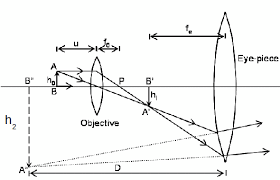
It has a series of two lenses; (i) the objective lens close to the object to be observed and (ii) the ocular lens or eyepiece, through which the image is viewed by eye. Light from a light source (mirror or electric lamp) passes through a thin transparent object.

The objective lens produces a magnified ‘real image’ (first image of the object). This image is again magnified by the ocular lens (eyepiece) to obtain a magnified ‘virtual image’ (final image), which can be seen by eye through the eyepiece. As light passes directly from the source to the eye through the two lenses, the field of vision is brightly illuminated. That is why it is a bright-field microscope.

The Magnification of a Compound Microscope

Determine the magnification of a compound microscope

The object lens forms a real and inverted image IIof the object O ( the image is slightly magnified). The eyepiece lens acts as a magnifying glass for the first image II and produces a magnifical virtual image.

The object is placed just beyond the principal (fo) of the objective lens so that that the real image I, is formed inside the principal focus (F) of the eye piece. The eyepiece treats the real image I, as an object and then forms its magnified virtual image I2.

Magnification of a compound microscope: This isthe ratio of the image distance produced by a compound microscope to the object distance. The magnification produced by objective lens is v/u.

Where

V is the image distance

U is the object distance

The magnification given by the eyepiece is given by;

Me = 25/fe + 1

If the final image is formed at the least distance of distinct vision (V = 25cm).

Mc = Mome

Combine eqn (i) and (ii)

Then

Mc = (v/u) (25/fe+1)

The above formula shows that the final virtual image is formed at the least distance of distinct vision.

Uses of a Compound Microscope

Mention uses of a compound microscope

The uses of a compound microscope includes the following:

• Used to magnify microorganism such as bacteria which cannot be seen by naked eyes.
• Used in hospitals widely to detect microorganisms in specimens provided by patients. A specimen is a small amount that is taken for testing. Blood is an example of specimens. In hospitals microscopes can detect parasites such as plasmodium ssp (a causative agent for malaria) in blood specimen.

Example 2

A certain microscope consists of two converging lenses of focal length 10cm and 4cm for the objective and eyepiece, respectively. The two lenses are separated by a distance of 30cm. The instrument is focused so that the final image is at infinity. Calculate the position of the object and the magnification of the objective lens.

For the objective lens

I/U + I/V = I/Fo

Where

Fo = 10cm

The objective lens forms a real image of the object at the principal focus of the eyepiece.

Thus

V = (30 – 4)

= 26cm

Thus I/U + I/V = I/10

I/U + 1/26 = 1/10

1/U = (1/10 – I/26)

(I/U) -1 = (4/65)

(1/U) -1 = (4/65)-1

U = (65/4)

The distance of object, U= 16.25cm

The magnification given by the objective lense is given by:

Whereas:

V = 26cm

U= 16.25cm

Mo = (26cm/16.25cm)

The magnificent given by objective lens, Mo = 1.6.

Astronomical Telescope

The Structure of an Astronomical Telescope

Describe the structure of an astronomical telescope

An Astronomical Telescope is used for observing heavenly bodies like stars and planets (generally bodies which are very far away from normal vision of human eyes ). Like compound microscope, it consists of two convex lenses, objective lens and the eyepiece.

The focal length Fb of the objective lens is longer than the focal length Fe of the eye piece lens.Rays of light from a distant object are nearly parallel when they strike the objective lens of the Telescope.The objective lens forms a real image, inverted and diminished image IQ of a distant object is in the focal plane.The eye piece forms the final magnified image at infinity

When the telescope is adjusted in such a way that the final image is at infinity it is said to be in normal adjustment.In this case the distance between objective lens and eyepiece is (Fb + Fe) This is the maximum separation between the objective lens and the eyepiece lens.

The Mode of Action of an Astronomical Telescope

Describe the mode of action of an astronomical telescope

The main reason for a distant object to be smaller is that the two objects subtend different angles at the eye. In other words, we can say that different angles substended by the eye causes a distant object to appear smaller.

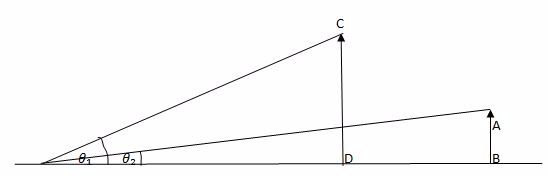
The object AB and CD are of the Same height.The object CD is closer to the eye than AB.

The object CD appears to be taller than AB because angle B that CD subtends at the eye is greater than the angle x subtended by AB at the eye. Images there can be made to appear large by bringing them closer to the eye.

In a telescope the final image is magnified because it subtends a much greater angle at the eye than does a distant object observed without a telescope. B is the angle subtended by the final image at the eye and X is the angle subtended by a distant object.

The Magnification of an Astronomical Telescope

Determine the magnification of an astronomical telescope

The magnification of a telescope is defined as the ratio of the angel B (in radians) subtended by the final image at the eye to the angle X subtended by a distant object at the eye.

Thus, for telescope the magnification is given by:

M = B/x ………………………………….i

From figure B= IQ/ID ……………………..ii

X = IQ/IA ………………………………………..iii

But Insert eqn (ii) and (iii) into eqn (i)

M = (12/ID)

(IQ/IA)

M = (IA/ID)

But IA = fo and IF =fe

M = fo/fe……………………………….(x)

Where

Example 3

fois the focal length of two thin converging lenses of focal lengths 25cm and 4cm respectively. It is focused on the moon which subtends an angle of 0.6° at the objective lens. The final image is formed at the observers least distance of distinct vision (25cm in front of the eyepiece). Find the diameter of this image.

In the previous figure:

X = h/fo

Where fo is the focal length of the objective lens

X = h/25

Where X is the angle in radians subtended at the objective lens by the moon.

H = 25x

H = 25 (6/10 x 11/180)

H = 25 (6/10 x 22/7 x 1/80)

H = 0.2619m

The height of the image, h = 0.2619m

The distance of this image from the eyepiece is obtained from the relation:

• I/U + I/V = I/fe = 4cm
• V= -25cmV = -25cm
• I/U – I/25 = ¼
• I/U = (1/4 + 1/25)
• (I/U)-1 = (25 +4) -1/100
• 100U= (100/29)

The magnification, m of the lens:

• M = V/u
• M = (25CM/100/29)
• M = 29/4

Let the height of the final image of the moon be h:

• M = Hi/h
• hI = mh
• HI = (29/4) (0.2619)
• HI= 1.90cm

The Height of image Hi = 1.9cm

Hence

The diameter of the final image of the moon will be 1.90cm

Observation of the universe today are best made from the Hubble Telescope. Outside the Earth’s atmosphere, this telescope suffer from less interference.

Uses of an Astronomical Telescope

Mention uses of an astronomical telescope

Astronomers use telescopes because they're much better than our eyes. Here are a few reasons:

1. Telescopes see lots of colours - telescopes can collect light that our eyes are unable to: radio, microwave, infrared, ultraviolet, x-rays and gamma rays.
2. Telescopes collect lots of light - our pupils are only a few millimeters across, so we can only collect photons over a tiny area whereas telescopes can collect photons of huge areas (e.g. a football fields worth for radio telescopes).
3. Telescopes see fine details because of the wave nature of light and the nerves in our eyes, we can only see details about the same angular size as Jupiter's width. Telescopes can allow us to resolve fine details - like Jupiter's Great Red Spot.
4. Telescopes can record observations with cameras - You can see things with your eye and draw them, but telescopes can share observations with the world! This is especially important for convincing skeptics that what you saw was real!

A Simple Astronomical Telescope

Construct a simple astronomical telescope

A simple telescope

Projection Lantern

The Structure of the Projection Lantern

Describe the structure of the projection lantern

The projection lantern forms images of slides or camera film onto a distant screen. The film or slide to be projected is inverted and highly illuminated.

The Mode of Action of a Projection Lantern

Describe the mode of action of a projection lantern

Optical arrangement of projection lantern.

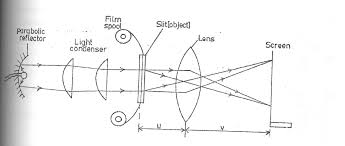
• The slice or film to be projected is inverted and highly illuminated.
• The concave mirror helps to concentrate the light which would otherwise be partly wasted.
• The lamp is placed at the principal focus of the concave mirror.
• The heat filter reduces the heat at falling on the slide or film so as to avoid it overheating.
• Since the image of the projection lantern is Highly magnified, it would not be very bright if there was not enough illumination.
• The condenser directs a maximum amount of light from the source of the slide and produce uniform illumination the screen. (The condenser is a double in order to reduce chromatic aberration).
• The projection lens forms the image of the slide on the screen.
• The light source is usually located at a distance of 2f from a condenser and invited so that the image on the screen is upright (erect).
• The focal length of the projection lens is ABOUT TWICE THE FOCAL length of the condenser since the screen is usually far from the lens.

The Magnification of a Projection Lantern

Determine the magnification of a projection lantern

Example 4

A lantern projector using a slide of (2cm x 2cm) projects a picture (1cm x 1cm) onto a screen 12m from the projection lens. How far from the lens must the slide be? Find the approximate focal length of the projection lens.

Solution

The magnification m is given by;

M = V/U ………………………………………i

Where

• HI is the size of image
• H is the size of object
• U object distance
• V image distance

Thus

M = Hi …………………. ii

Then eqn (i) = eqn ii

• v/u =hi/h
• (1200/u)-1 = (100/2) -1
• (u/1200) = (2/100)
• U = (2/100) (1200)
• U = 24cm

The object distance, U = 24cm

Uses of a Projection Lantern

Mention uses of a projection lantern

Projection lantern are used in various areas. These include:

• Projection of films, slides and transparencies,
• projection of opaque objects, i.e. episcopic projection,
• used in searchlights and headlights,
• used in projection apparatus in industry for gauge and screw thread testing,
• used in physical experiments such as projection of a spectrum,
• used in polarisation experiments and interference experiments.

A Simple Projection Lantern

Construct a simple projection lantern

Projection Lantern

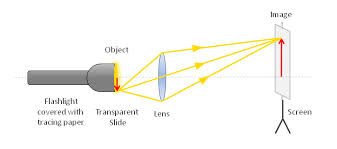
The Lens Camera

The Structure of the Lens Camera

Describe the structure of the lens camera

Lens camera is an instrument which produces an image of object on the screen using light. The basic physical principle of all camera is the same in spite of the variation in the design of cameras.

The optical system of the camera are very similar to that of the lantern projector but with the direction of light reversed.The converging lens forms a real image of the object to be photographed.(This image is diminished (smaller than the object and inverted)

<!--[endif]-->The lens can be moved back and forward with the help of focusing any so that objects at different distances can be brought to the focus.A forced image is locate on the film or plate when the shuttled is open for a suitable amount of time as determined by the shutter speed.

<!--[endif]-->Light enters the camera Box and makes a picture of the object on the film “( The film is sensitive to light)

<!--[endif]-->The camera is equipped with a diagram or light entering the camera.It ensures that is incident centrally on the lens so that the distortion of the image formed is reduced

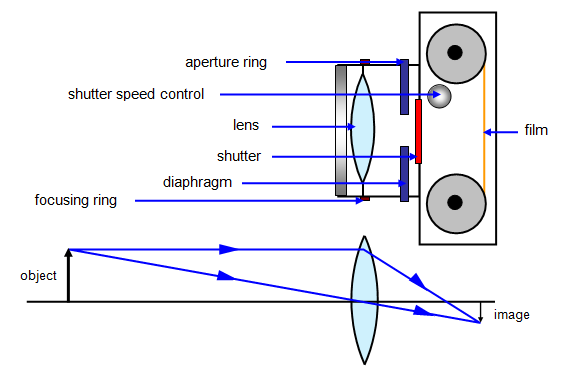
The Mode of Action of the Lens Camera

Describe the mode of action of the lens camera

The aperture stop, which is the limiting diameter of the aperture thought which light enters the camera (given as fraction of focal length F of lens) is also called F Number.

This F Number; is the fraction of focal length of the lens given as focal length divide by lens diameter.

F number = Focal length, F/Lens diameter, d

FN = F/d

Where d = is lens diameter.

• The Number Indicates the Number of times the focal length F of times the focal length F of the lens diameter ( or stop)
• The smaller the F - Number for a given focal length the larger the lens diameter
• The lens with a larger diameter has a greater light- gathering power or speed
• This for such a lens the shutter allows light in the camera for a short interval of time.

The Magnification of the Lens Camera

Determine the magnification of the lens camera

Magnification of a lens camerais obtained as the ratio of the Image distance and the object distance.

But from the lens formula:

Thus M = v/U

I/U + I/V = I/F

I/V = I/F - I/U

(I/V) –I = ( U - F / FU)-I

V = FU/ ( U - F)

Example 5

A lens camera is to be used to take a picture of a man 2m tall if the lens of the camera Has a focal length of 10cm, calculate the minimum size of the film frame required, given that the man is 20.1m from the camera.

Solution:

Magnification is given by:

M = f/ (u-f)

Where

F= 10cm U = 201/m / 2010cm

M = ( 10/2010 – 10)

M = 1/20 ....................................i

Let the size of the frame be h when the height of man is 2m.

Then

M = 1/200

But h1/h = 1/200

h1 = (1/200) 2

h1 = (1/200)2

h1 (2/200)

h1 = (1/100) m

h1 = 1cm or 10mm

The film frame should be at least 10mm square.

Simple Lens Camera

Construct a simple lens camera

A simple lens camera

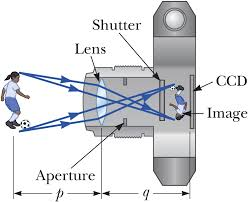
The Human Eye

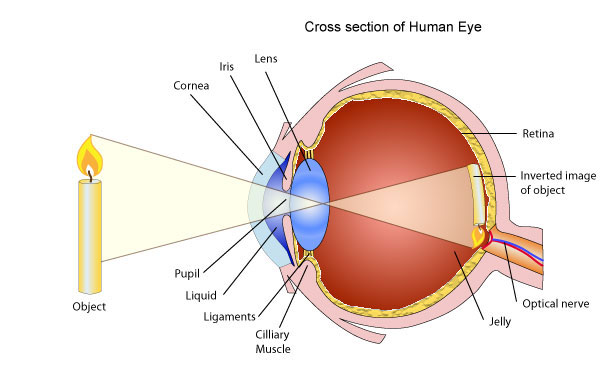
The Structure of the Human Eye

Describe the structure of the human eye

The eyeball approximately spherical in shape.The wall of this sphere consist of two layers, the outer layer or sclera and the inner layer or choroid.The front portion of the SCLERA FORMS A TRANSPARENT CURVED section called the camera.The choroid layer is balance in order to prevent internal reflection and also to protect the light sensitive parts of the eye.

The aqueous and vitreous hum our are jelly – like substance that fills the spaces within the eyeball.The aqueous humour is the salt solution of refractive index n, 1.38.Vitrous hurmour is a watery , Jelly substance of refractive index 1.34.Behind the cornea there is a colored diagram called the iris.

The iris has the central hole called the pupil. The iris contains muscles which control the size of the pupil. The size of the pupil decreased in the bright light and increased in the dim light.

Behind the pupil and there is a crystalline lens held in position by suspensory ligaments that are attached to the choroid layer.Near the suspensory ligaments are the ciliary muscles.The function of the suspensor ligaments there are the cilliary muscles.

The function of cillary muscles is to control the thickness of the lens. The lens become thick when the ciliary muscles contract and thin when the ciliary muscles are relaxed.

<!--[endif]-->At the back of the eye there is a retina (This is the part of the eye which is sensitive to light).Image formed is inverted formed on the Retina ( This is the part of the eye which is sensitive to light.)

Image formed is inverted formed on the retina by successive refraction of light at the corner, the aqueous hurmour the crystalline lens and the Vitreous hurmour.Electrical signals are then transmitted to the Brain through the topic nerve. Finally, the brain interprets these signals.

Accommodation Power of the Human Eye

Explain accommodation power of the human eye

Accommodation is the process whereby the eye alters its focal length in order to form images of objects at different distances.

(Thickening or Thinning of the lens causes a change in its focal length).

The thickening or thinning of the crystalline lens is made possible by the action of the ciliary muscles.To view neare object t, ciliuary muscles contract, this makes the lens thicker.

In the relaxed state of ciliary muscles, the crystalline lens become thinner and enables the eye to see (view) distant objects. The farthest point which can be seen clearly is called the far point of the eye and the nearest point is called the near point of the eye.

The corresponding distance from these points to the eye are referred to as the maximum and least distance of district vision respectively.A normal eye (i.e. without defects of vision) has a far point at infinity and near point at a distance of 25cm from the eye.Structure of lens “ view distant object”

The Defects of the Human Eye

Identify the defects of the human eye

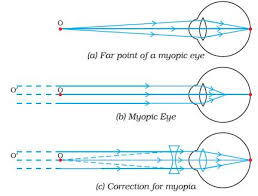
Myopia or near-sightedness

• This defect causes person to see near object clearly while distant objects are not seen clearly.
• The strength of the cornea and the eye lens combination is too great even when muscles of the eye are completely relaxed.
• The focal length of the cornea and the eye – lens combination is always less than the distance to the retina.
• Images of distant object are formed in front of the retina even when eye is totally relaxed. However, an object that is closer can be brought into focus.
• In this situation the focal length of the cornea and the eye lens is so short that objects closer than the conventional (near point of 25cm) can be brought into focus. That’s why this condition is called Short sightedness (near sightedness).
• Since the problem is that the strength of the eye – lens and the cornea combination is too great, the solution is to provide eye glasses (or contract lenses) with negative lens.
• The negative lens weakens the strength of the cornea and eye – lens just enough so that the resulting focal length when the eye muscles are relaxed matches the distance back to the retina so that distant images are now in focused.
• The eye glass lenses are negative lenses that means they are thinner in the middle than at the edges.
• It is easy to identify this kind of eye glass lenses since acting by themselves they do not form a real image of an object at any distance.

Hyperopia or far-sightedness

• This defect causes a person to see distant objects only and short-distance objects are not seen clearly.
• In the person with this condition, the strength of the cornea and the eye-lens combination is too weak when the eye muscles are totally relaxed. So the image of a distant object is formed behind the retina.
• The solution in the opposite of myopia. Victims should wear positive eye lenses which strengthen the corner and the eye lens just enough so that the resulting focal length when the eye is relaxed matches the distance to the back of the retina.

Astigmatism

• This occurs when the focal length for the cornea and the eye's lens for an object oriented in some direction is not the same as for another located in a perpendicular direction.
• The eye can not bring the vertical and horizontal lines in a ‘+’ symbol in sharp focus at the same time. (The axis of differing focal length need not be exactly horizontal and vertical).
• The problem is that the cornea of the eye lens is not symmetrical. The solution is to use eye glasses whose lenses are not symmetrical in a complementary way.
• The cylindrical lens may be combined with an additional positive or negative lenses.

<!-- [if gte mso 9]><xml> Normal 0 false false false EN-US X-NONE X-NONE MicrosoftInternetExplorer4 </xml><![endif]--> Decreased accommodation

• This condition typically occurs in middle-aged people.
• The eye muscles gradually weaken with age, so that the range or accommodation is decreased.
• People with this condition cannot bring both near objects and far objects into focus.
• The weakening of the eye muscles often causes the focal length of the eye lens to increase as well so that many people of middle age tend to become far sighted.
• Since the problem is adequate accommodation, no single lens can correct it and people with this problem usual needs bifocals.
• Bifocals are glasses with two different lens strengths, one for near and one for distant objects.
• The usual arrangement is that the bottom half of the lens is the near strength and the top half is the far strength.

The Correction of the Defects of Human Eye

Describe the correction of the defects of human eye

Myopia is common name for impaired vision in which a person sees near objects clearly while distant objects appear blurred. In such a defective eye, the image of a distantobject is formed in front of the retina and not at the retina itself. Consequently, a nearsighted person cannot focus clearly on an object farther away thanthe far point for the defective eye.

This defect arises because the power of the eye is too great due to the decrease in focal length of the crystalline lens. This may arise due to either

1. excessive curvature of the cornea, or
2. elongation of the eyeball.

Correction:Thisdefectcan becorrectedby using aconcave (diverging) lens. A concave lens of appropriate power or focal length is able to bring the image of the object back on the retina itself.

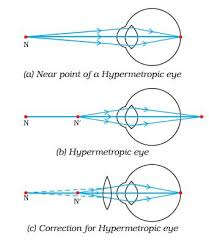
Farsightedness, also called hypermetropia, common name for a defect in vision in which a person sees near objects with blurred vision, while distant objects appear in sharp focus. In this case, the image is formed behind the retina.

This defect arises because either

1. the focal length of the eyelens is too great, or
2. the eyeball becomes too short, so that light rays from the nearby object, say at point N, cannot be brought to focus on the retina to give a distinct image.

Correction:This defect can be corrected by using aconvex(converging) lensof appropriate focal length. When the object is at N’, the eye exerts its maximum power of accommodation. Eyeglasses with converginglenses supply the additional focussing power required for forming the image on the retina.

The Human Eye and the Lens Camera

Compare the human eye and the lens camera

The camera

1. The eye and the camera has a have a convex lens which form a real and inverted image of an object.
2. The eye and the camera are blackened inside to prevent internal reflection. Rays of light which are not received on the retina or camera film are absorbed by the choroid layer of the eye or the black surface inside the camera.
3. The eye can regulate the amount of light that passes through the crystalline lens by using pupil while in a camera the diaphragm regulates light.
4. In the eye the image is formed in the retina while in the camera the image is formed on the photographic plate.
5. The eye can change the focal length of its lens by the contraction and relaxation of the ciliary muscles. In this way the eye can focus objects at different distance. In a camera objects at different distance are focused on by moving the lens forwards and backward