FORM ONE PHYSICS STUDY NOTES TOPIC 7-9.
TOPIC 7: PRESSURE
Concept of Pressure
Pressure in Liquids
A liquid will exert pressure on an immersed object as well as on the walls of the container holding it. Note that the pressure exerted by liquids is due to the weight of the liquid. Also increase in water level in liquid cause increase in pressure.
The Characteristics of Pressure in Liquids
Describe the characteristics of pressure in liquids
Note: Pressure in liquids =Force/Area
But force= hApg/A
=Hsg
Hence pressure in liquids is given as hsg.
H= Height of the liquid column
A= Area of the base
The pressure at any point in a liquid at rest then depends
- Depth
- Density of liquid
Note: It does not defend on the area
Pressure in liquids is characterized using the following parameters
- Pressure in a liquid increase with depth
- Pressure in a liquid acts equally in all directors
- Pressure in a liquid increases with increase in density of the liquid.
Mercury exerts more pressure than an equal volume of water. This because mercury is denser than water.
The Variation of Pressure with Depth in Liquids
Examine the variation of pressure with depth in liquids
Demonstration of water spurting from holes at different heights.
As pressure at point A is low due to small height of water above it but at point B the height increase and the distance of water increase while at point C the height is greatest therefore the level of water distance will be large distance.
Demonstration of pressure in a communicating vessel
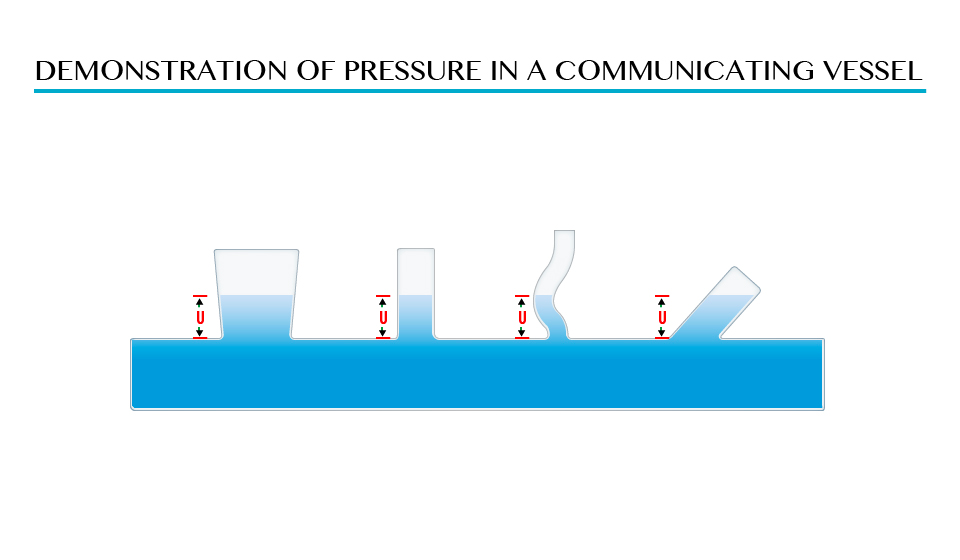
The shape of vessel found in point A, B, C and D is different but the pressure is the same due to the equal height (L) of the liquid above the points.
Problems Involving Pressure in Liquids
Solve problems involving Pressure in Liquids
Example 4
A cube of side 2cm is completely submerged in water so that the bottom of the cube is at a depth of 10cm. use g=10m/s2 and s=1000kg/m3
- What is different between the pressure on the bottom of the cable and the pressure on its tap?
- Determine the difference in the force on the top and bottom.
- What is the weight of the water displaced by the cube?
Solution;
Data.
Depth = 10cm = 0.1m
s = 1000kg/m3
g = 10m/s
h= 8cm= 0.08
formular
p= sgh
p=1000kg/m3x10m/s2x0.1m=1000N/m2
At the h= 0.08m p= 1000x10x0.08= 800N/m2
Change in pressure = 1000N/m =200N/m2
So that different in pressure between the bottom the top is 200N/m2
Pressure = Force/Area = P= F/A
Area =L2= (10.02)2= 0.0004m2
Distance in water 200N/m2x0.0004m2
This is the upthrust acting on the cube
Water displaced by the cube in weight= volume of the cube
Volume = l3 (2cm) 3 = 8cm3
For water, 1cm3= 1g 50.8cm3 = 8g
Weight of displaced water
mass of displaced water/100=8g = 0.08N
Example 5
Calculate the pressure at the bottom of tank of water 15m deep due to the water above it is (s=1000kg/m3).
Solution:
Data:
Height =15m
S=1000kg/m3
g= 10m/s2
Formula
Pressure in liquid sgh
= 1000x10x15=150000N/M2
The Principle of a Hydraulic Pressure
Explain the principle of a hydraulic pressure
It state that “Any external pressure applied to the surface of an enclosed liquid will be transmitted equally throughout liquid.”
Illustration of Pascal’s Principle.
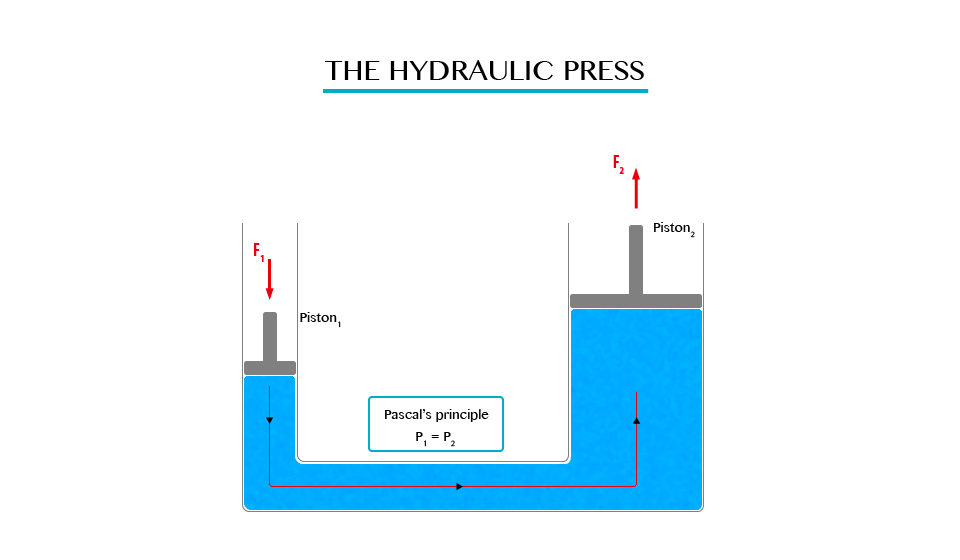
Note: in all side of vessel will experience equal pressure.
The hydraulic press works on Pascal’s principle, when using this principle a small force converted into a large force and vice versa.
From Pascal’s Principle
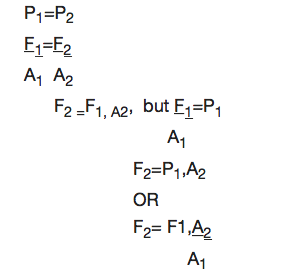
Note: The distance moved (d) is inversely proportional to the cross sectional area.
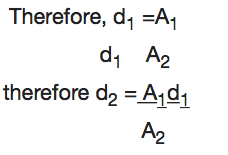
Example 6
The pistons of a hydraulic press have their areas given as 3.0x10-4m2 and 2x102m2 respectively. If the smaller piston is pushed down with a force of 12N, what is the force required to push the larger piston?
Soln:
Data:
F1 = 120N, A2= 2X102m2
A2 = 3X104m2
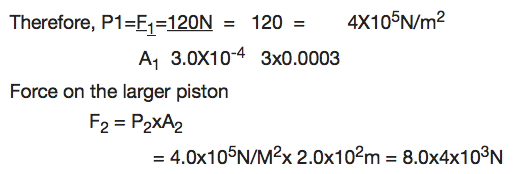
Application of Hydraulic Press
Measure pressure of a liquid
Hydraulic press is used in industries to express bulk items.
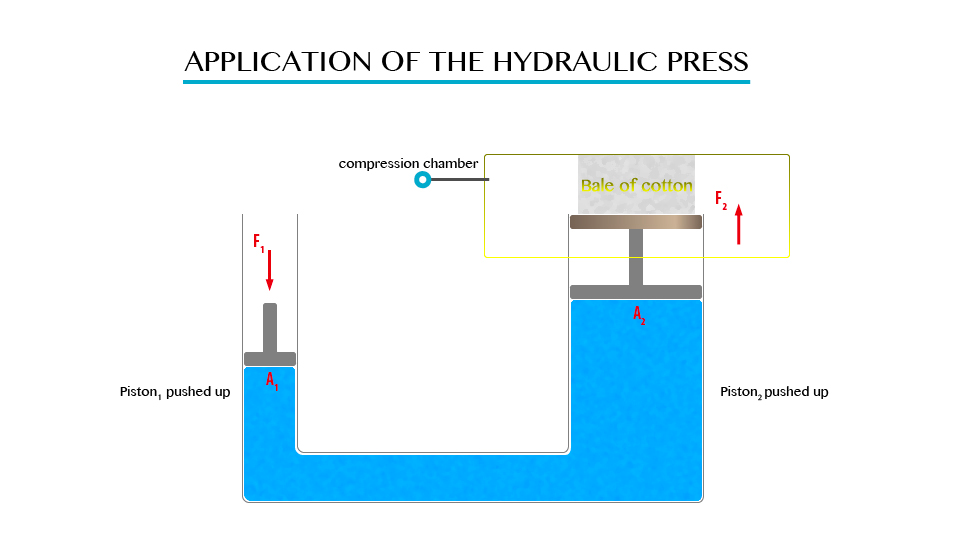
Hydraulic brake system
When pressure is applied to the brake pedal, it pushes the piston in the master cylinder forward creating a pressure in the brake fluid. This pressure is transferred to the slave cylinders where it is multiplied and pushes the brake shoes against the brake dram that is attached to the wheel of the vehicle.
It is used in industries in the forming of metals.
Since the hydraulic press act like a lift, it is used for lifting heavy loads.
Measuring the pressure of liquids using a manometer. Manometer is the device for measuring pressure (commonly gas).
Atmospheric Pressure
The Existence of Atmospheric Pressure
Describe the existence of atmospheric pressure
Atmospheric pressure is as a result of the weight of this layer of gases, the act at atmospheric pressure is surrounded the layer of air consisting of a mixture of gases.
Note. The atmospheric pressure on the earth’s surface and objects on the earth is a approximately 1.01x105N/m2.
The experiment which demonstrate the existence of atmospheric pressure.
Umbler experiment
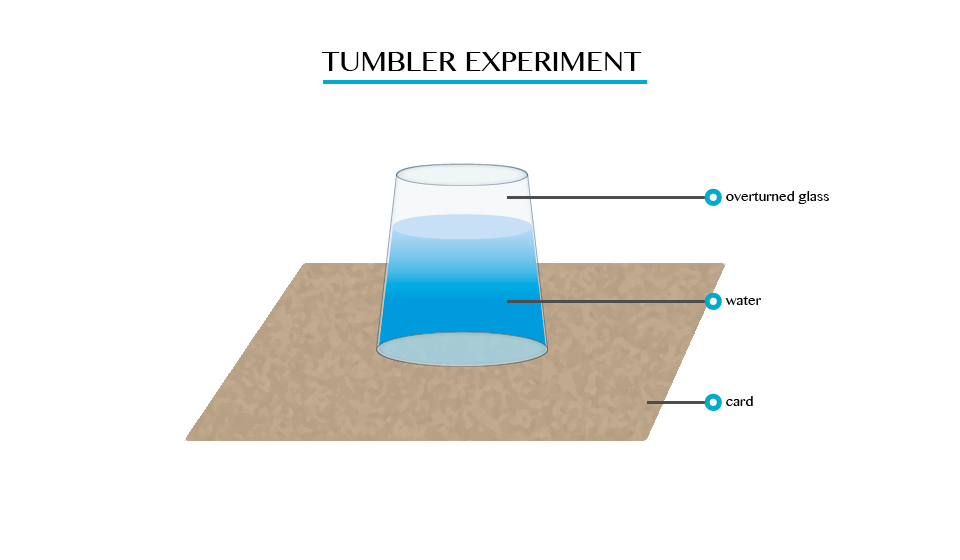
When you fill a glass timber with cord and gentle turned upside down. It will be seen that water will not poured down.
Plunger
Pulling the plunger is not easy. This is so because all the air is squeezed out from the table when the surrounding pressure being high the plunger sticks.
Crushed bottle
When putting hot water in, the bottle is cooled under cold water the steam condenses; leaving partial vacuum inside the bottle consequently the greater atmospheric pressure outside the bottle crushes it in wards.
Applications of Atmospheric Pressure
Identify the applications of atmospheric pressure
A siphon
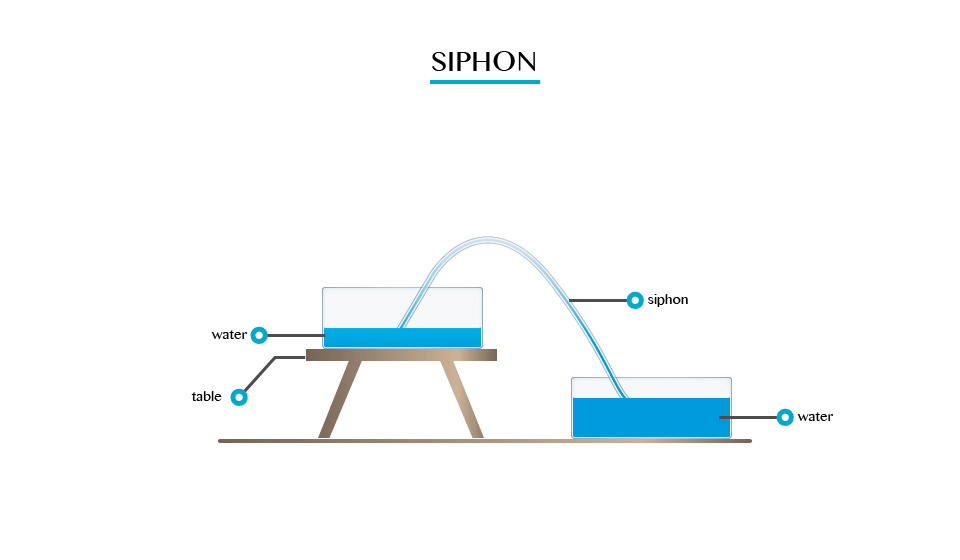
A siphon is applied in areas and devices that we use everyday
- It is used in the toilet flushing cisterns (chain and ball tank). The flush is triggered by a handle that operates a simple diaphragm like piston pump that lifts enough water.
- It is used in special rain gauges called siphon rain gauge which are able to automatically drain out excess water.
- A siphon cup is a reservoir attached to a gum.
- It is used is some drainage systems to drain water to one point.
The lift pump
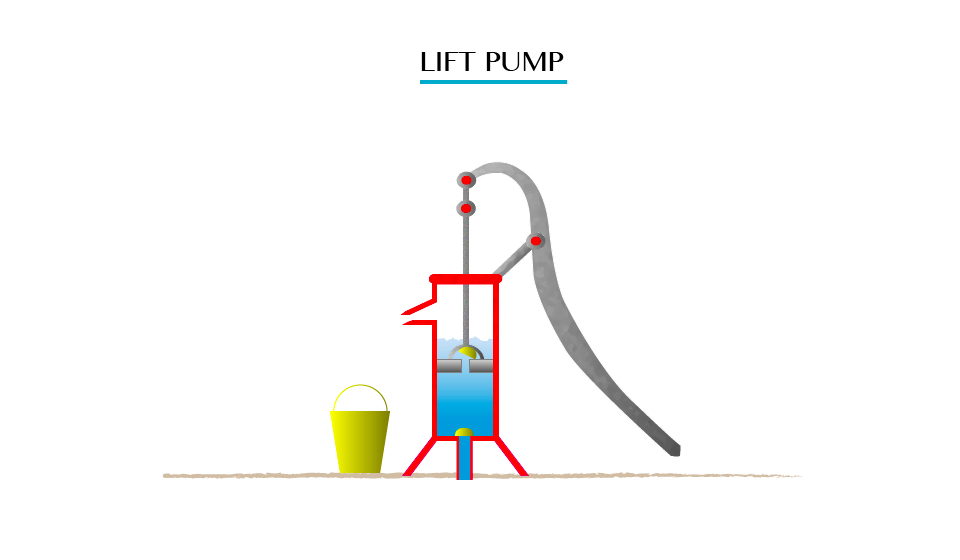
A lift pump is used to raise water from underground sources. This is a pump that is used to lift the liquid, rather than force liquid up.
A syringe is a simple piston pump that lifts a tube. The plunger that lifts can be pulled and pushed through inside a cylindrical tube or barrel. This enables the syringe to take in or expel fluid through the opening (nozzle) at the end of the tube.
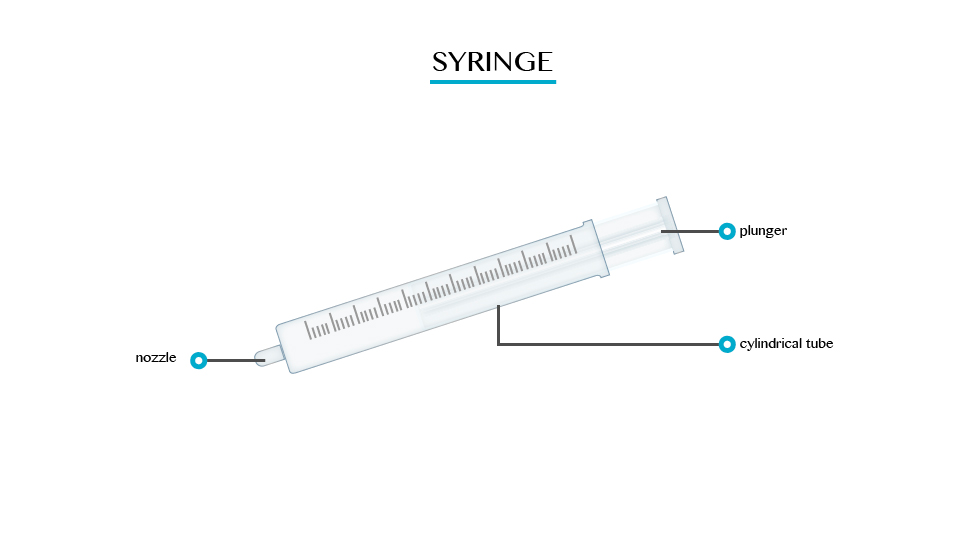
Uses of syringe:
- They can be fitted with hypodermic needles and used to administer injections.
- They are used to measure liquids and gases in a laboratory.
- They are used to apply certain compounds such as a glue or lubricant.
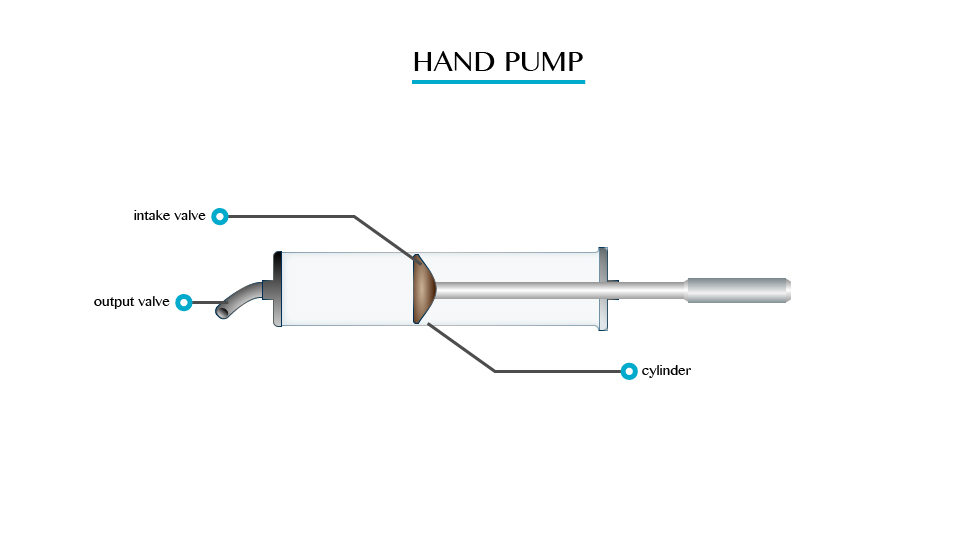
Bicycle pump
This is a type of force pump that consists of a hollow metal cylinder and a movable piston.
Meassuring Atmospheric Pressure
Measure atmospheric pressure
Atmospheric pressure is measured by using barometer;
Types of barometer:
- The simple barometer
- Fortin barometer
- Aneroid barometer
This is a type of force pump that consists of a hollow metal cylinder and a movable piston.
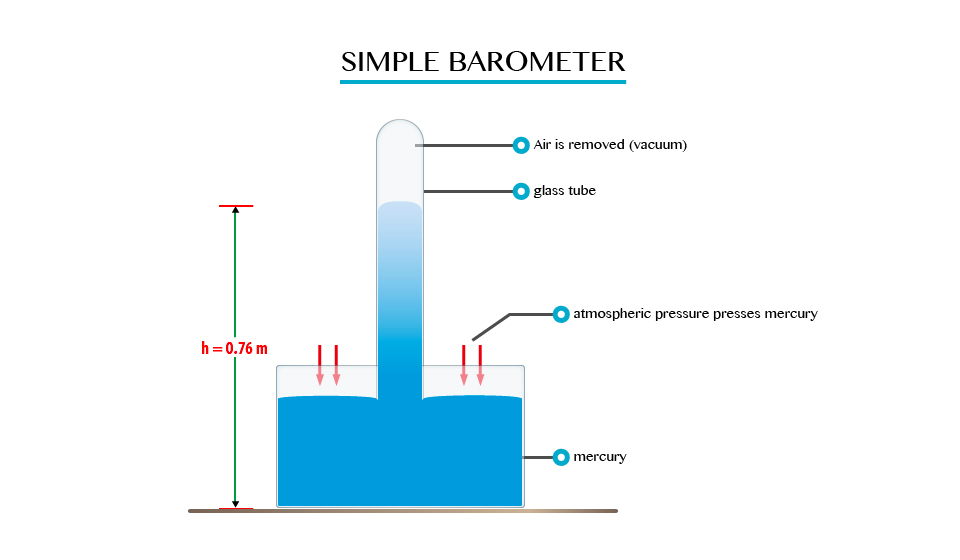
A simple barometer is the most fundamental of the other types of barometer. The barometric liquid used is mercury.
A simple barometer consists of a hard glass tube closed at one end.
Fortin barometer
A Fortin barometer is a modified simple barometer. It consists of an inverted tube closed at its upper end with the lower open end immersed in a reserve of mercury. The atmospheric pressure is measured in terms of the height of the column of mercury.
Disadvantages of Fortin barometer:
- Mercury is very expensive to use and is very toxic. For these reasons, an aneroid barometer is usually preferred.
- It is not portable as it is generally big and contains liquid.
- It must be mounted in a vertical position.
Work
Energy
The Concept of Energy
Explain the concept of energy
Energy can be defined as capacity of doing work.
Energy has the same SI unit like that of work, and that is Joules (J)
S.I Unit of Energy
State S.I unit of energy
Energy has the same SI unit like that of work, and that is Joules (J)
Different Forms of Energy
Identify different forms of energy
There are different forms of energy such as:
- Chemical energy
- Heat energy
- Light energy
- Sound energy
- Electrical energy
- Nuclear energy
- Solar energy
Difference between Potential Energy and Kinetic Energy
Distinguish between potential energy and kinetic energy
There are two types of chemical energy, which are:
- Potential energy:It is the energy possessed by a body mass in its position or state.
- Kinetic energy: It is the energy possessed by a body due to its motion.
Consider when the body is vertically thrown upwards with an initial velocity ‘u’ from the ground.
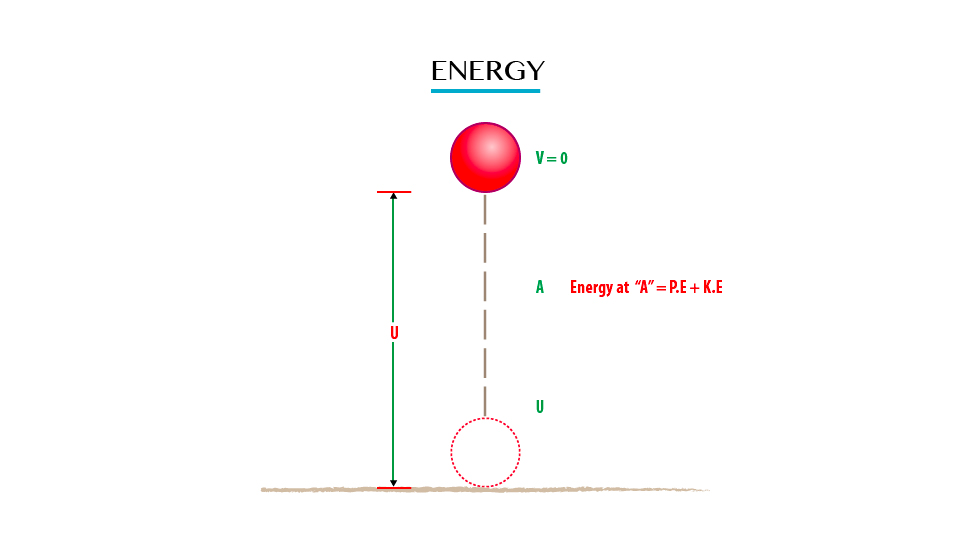
At the ground:The height is zero and initial velocity is at maximum so as to attain maximum height.
Therefore K.E = ½ MV2 will be maximum
K.Emax = ½ mv2
Where K.E = Kinetic energy
M = Mass of the object/body
V=Velvety
P.E = Mgh
Where
P.E = Potential energy
M= Mass of the object
H = Height of the object
g = gravitation force
P.E = Mgh will be zero because P.E
= M*g*0 (body at the ground where k=0)
Neglecting the air resistance, as the body moves upwards its velocity decreases it also experiences gravitational force (g) pulling downwards towards the earth’s centre.
The maximum Height Attained
The final velocity of the body will be zero (V=0)
Therefore K.E = ½ mv2
K.E = ½ m(0)2
K.E = 0
P.E = MgHmax
Note:That the object drops from Hmax that is; it leaves with zero Kinetic Energy. At position A in fig. 8. The conservation of mechanical energy (M.E) is given as:
P.E + K.E = Constant
(The sum of P.E and K.E is constant throughout the motion of the object if the air resistance is neglected)
The Transformation of Energy
Explain the transformation of energy
The notion of energy is that energy is changed from one form into different forms using transducers.
Transducer is a device used to transform energy from one form to another.
For example:
- Battery converts chemical energy into electrical energy.
- A generator converts mechanical energy into electrical energy.
- A motor converts electrical energy into mechanical energy.
The Table Summarising Energy Transformation
| ORIGINAL ENERGY | TRANSDUCER | ENERGY TRANSFORMED |
| Chemical energy | Battery | Electrical energy |
| Chemical energy | Motor | Chemical energy |
| Mechanical energy | Generator | Electrical energy |
| Solar energy | Solar panel | Electrical energy |
| Chemical energy | Motor car | Mechanical energy |
| Electrical energy | Microphone | Sound energy |
| Electrical energy | Heater | Heat energy |
Activity 1
To demonstrate pressure of potential energy.
Materials and Apparatus
- A heavy stone
- A bucket full of water
- A strong inelastic rope; and
- Smooth pulley
Procedures:
- Collect the heavy stone, using a strong rope tie it to a bucket of water
- Pass the rope over smooth pulley fixed to a support.
- Hold stationary the heavy stone at height “h” above the ground
- Release the stone
Results and observations:
- When the stone released the bucket of water will start to rise.
- The stone is said to have potentials energy because of its position above the ground.
- Lifting a body of mass “m” to a height “h” above the ground requires work to be done against gravity. Work = Mgh
Example 2
A ball of mass 0.5 kg is kicked vertically upwards and rises to a height of 5m. Find the potential energy by the ball.
Data given:
Mass of the ball (Mb) = 0.5 kg
Height (h) = 5m
Gravitation force (g) 10N/kg
Potential energy (P.E) = ?
Solution:
Potential energy (P.E)= mgh
= 0.5kg x 10N/kg x 5m
= 25 NM
1NM= 1Joules
Potential energy (P.E) = 25 Joules.
Activity 2
Aim: to investigate the law of conservation of energy by a simple pendulum.
Materials and Apparatus:A pendulum bob and light inelastic string.
Producers
- Pull the bob of a simple pendulum in position A so that it is at height “h” above position B.
- Release the bob so that it swings to position C via the lowest position B and back to A.
- Consider the figure below:
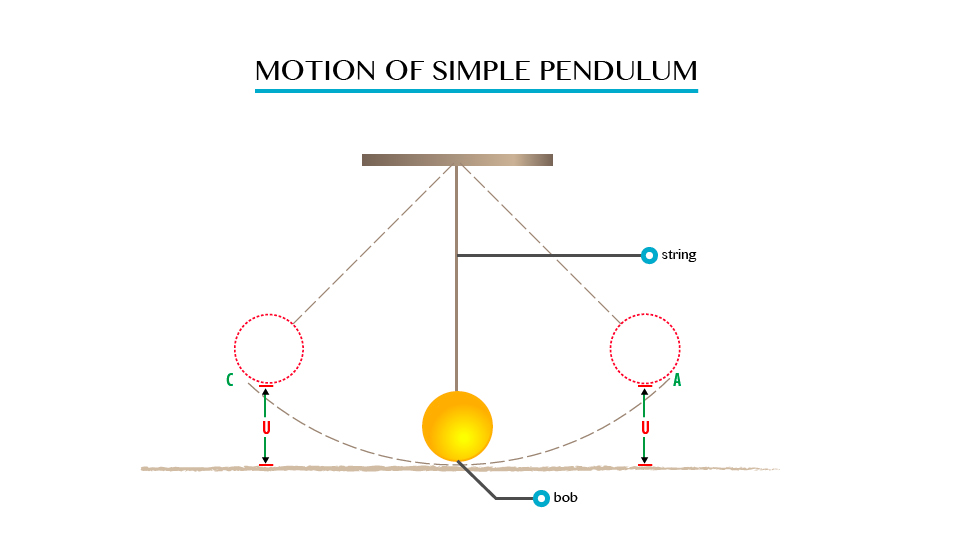
Observation
When the bob is at position A, it possesses potential energy only due to the height “h” which is equal to “Mgh”.
As it swings downwards to position B, the height decreases, and as the result it loses potential energy.
- The bob has Vmax and hence K.Emax at B. The height at B is zero, thus the P.E is zero.
- As it swings towards C, the P.E increases and reaches its maximum again in position C, where the Kinetic Energy is zero. At position D, the energy of the bob is party potential and party Kinetic.
The Principle of Conservation of Energy
State the principle of conservation of Energy
The law of conservation of energy state that “ Energy can neither be created nor destroyed but can only be converted from one form to another.”
This means the amount of energy is constant all the time.
Example 3
A stone of mass 2kg is released form a height of 2m above the ground. Find the potential energy of the stone when it is at the height of 0.5m above the ground.
Data given;
Mass of the stone (Ms) = 2kg
Height released (h) = 2m
Gravity (g) = 10N/kg
Potential energy = (P.E) ?
Solution:
P.E at height g 2m
P.E = Mgh
= 21g x 10N/kg x 2m
P.E = 40 Joules
P.E at 2m = 40Joules
Than P.E at height of 0.5m
= 21g x 10N/kg x 0.5m
P.E at 0.5m = 10Joules
100s of P.E = 40 Joules - 10Joules
= 30 Joules
According to conservation of energy the loss of P.E should be equal to the gain in K.E, when the air resistance is neglected.
K.E of the stone at 0.5 above the ground = 30 Joules
Example 4
A ball of mass 0.21kg is dropped from a height of 20m. on impact with the ground it loses 30J of energy. Calculate the height which it reaches on the rebound.
Data given;
Mass of ball (Mb) = 0.2kg
Height dropped (h) = 20m
Loose in energy (E) 30J
Height which reaches=?
Solution;
Consider the figure below;
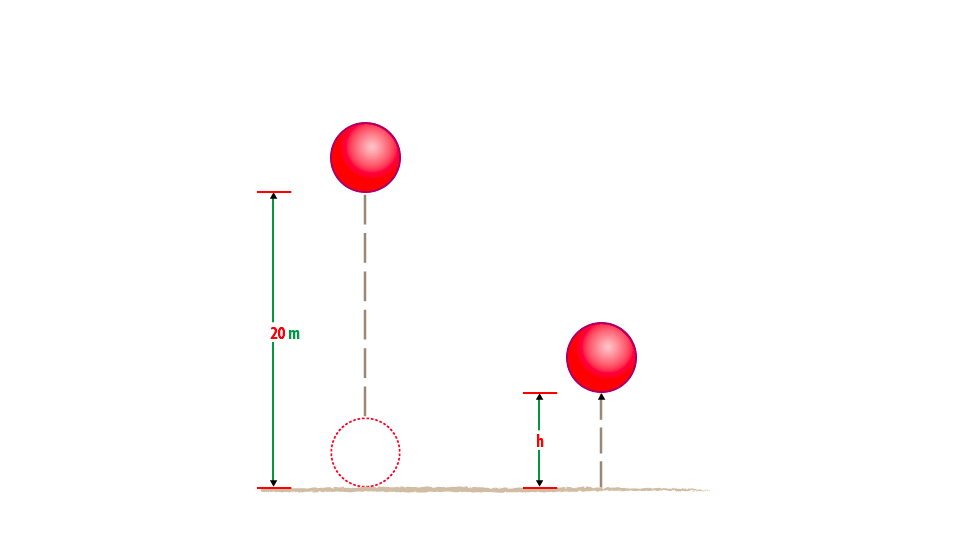
At 20m above ground the initial energy of the ball = Mgh
= 0.2kg x 10N/kg x 20m
= 40 Joules.
So after the impact the ball loose 30J and the energy remaining is 40 J-10J
= 10Joules
At the top of rebound the energy of the ball = potential energy (P.E)
The height reaches (h) is 5m.
Uses of Mechanical Energy
Explain the uses of mechanical energy
The mechanical energy can be used to produce electric power using generators. Some uses of mechanical energy are: It enables our body to do work, it makes work easier and faster, it is used to transport goods and people from one place to another, many transport vehicles uses the knowledge of mechanical energy. Examples of vehicles which uses mechanical energy are aeroplanes and motor cars.
Power
The Concept of Power
Explain the concept of power
Power is the rate of which work is done.
- It is a measure of the rate at which energy changes.
- This means that whenever work is done energy changes into a different form.
The S.I Unit of Power
State the S.I unit of power
The SI unit of power is Jules per second J/S or watts, W.
1 Joules per second = 1 watt
When 1 Joules of work is done per second the power produced is a watt. Watt is the unit for measuring electrical power.
The Rate of Doing Work
Determine the rate of doing work
Suppose that two cranes each lift objects having masses of 200kg to a height of 12m. Crane A lifts its object in 10sec while crane B requires 15sec to lift its object. Assume they lift the objects at a constant velocity they do the same amount of work.
Work done = GPE
= Mgh
= (200kg) (9.8m/s2)(12m)
= 23520J
Each did a work that was equivalent to 23520J.
What is different for the two cranes is the rate at which they did the work or their generation of power.
The power of crane A can be calculated by;
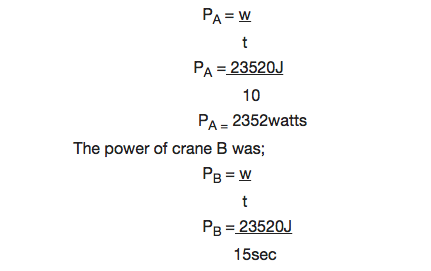
PB = 1568 watts.
Example 5
How much power is required to accelerate a 1000kg car from rest to 26.7m/s in 8sec?
Solution:
The work done on the car increases its Kinetic energy.
Work done = AKE
½ MV2 – ½ MV2
The power required is given by:
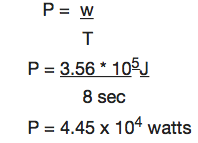
Example 6
Car engine is rated in horsepower (hp) where 1hp = 746watts. What is the required power measured in horsepower?
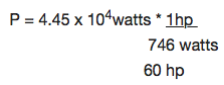
Since work causes a change in energy. DE power can be considered as the rate of change of energy.
P = DE/t
TOPIC 9: LIGHT
Propagation and Transmission of Light
The Concept of Rays and Beam of Light
Explain the concept of rays and beam of light
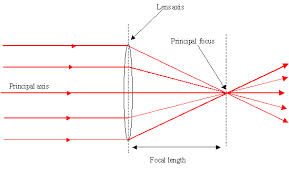
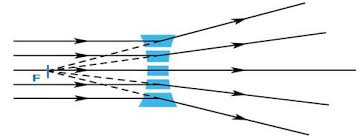
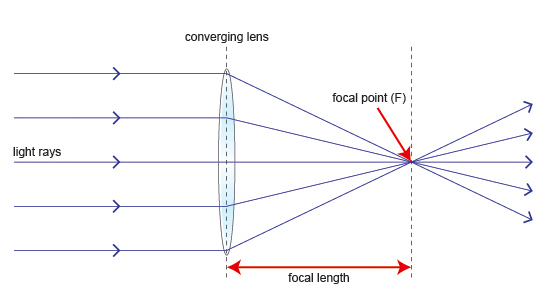
A straight line showing a path of light is called a ray which is the direction of the path taken by light. Rays of light are represented in diagrams by full straight line with arrow marking the direction in which the light is travelling
A beam is a stream of light rays, and it is usually represented by a number of rays. Rays of light can converge (converging rays) or they can diverge (diverging rays)
A ray of light
Parallel rays
Diverging rays
Converging rays
Verification that Light Rays Travel in Straight Line
Verify that light rays travels in straight line
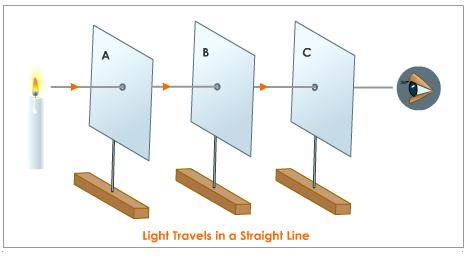
Activity 1
Aim: To demonstrate the rectilinear propagation of light.
Materials and apparatus
- The pieces of card board with a hole in each.
- Source of light, eg. a candle.
Procedures:
- Put the pieces of cardboard with the holes in a straight line.
- Arrange them to a distance of about 50cm apart.
- Place a lighted candle at one end of cardboard A. observe the light from behind cardboard C.
- Now displace any one of the pieces of cardboard, eg. Cardboard B.
Propagation of light in straight line.
Observations
When observing from card C, the candle can be seen. Displacing any one of cardboards, the candle can no longer be seen as the holes are no longer in a straight line. This happens due to the fact that light travels in a straight line.
Transparent, Translucent and Opaque Materials
Identify transparent, translucent and opaque materials
Objects can be grouped according to transmission of light through them, ie. The degree passage of light as light rays falls on their surface.
Opaque bodies
These are bodies which do not allow light to pass through them, ie. Stones, wood, concrete walls and bodies.
Translucent bodies
These are bodies which allow small amount of light falling on them to pass through e.g oiled paper, some plastic materials and tinted glass.
Transparent bodies
These are bodies which allow all light to pass through them, e.g glass, pure water and air. The transmission of light through different bodies can be investigated by performing other experiment.
Activity 2
Aim: To investigate transmission of light.
Materials
- Sheet of paper
- Sheet of glass
- Tinted glass
- Card board
- Oil paper
The Concept of Reflection of Light
Explain the concept of reflection of light
Reflections are obtained from hard and highly polished surfaces such as mirrors and sheets of glass than from rougher surfaces, when light falls on the surface at an inclined plane angle, it is sent back into the air. This is also the case when light falls on all highly polished metals. If light falls on a polished surface at an angle 900, it is sent back into the air on the same path.
Difference between Regular and Irregular Reflection of Light
Distinguish regular from irregular reflection of light
Surface can be classified into two types:
- Highly polished surfaces, examples are mirror, polished cooking utensil and silvered iron sheets.
- Rough surface, examples are unpolished wooden table, sheet of paper and cobblestone road.
Application of the Laws of Reflection of Light
Apply the laws of reflection of light
Reflection is guided by some natural laws called “Laws of reflection” the Laws of reflection state that:
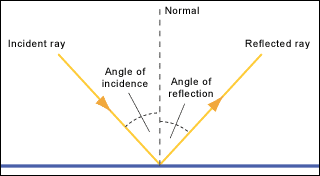
- The incident ray, the reflected ray, and the normal at the point of incidence all lies in the same plane.
- The angle of incidence is equal to the angle of reflection.
Image Formed by a Plane Mirror
Describe image formed by a plane mirror
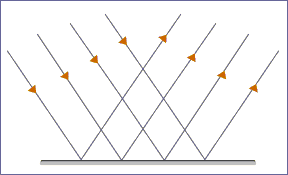
A clear image is recognised as a result of reflection of the beam striking the highly polished surfaces. This is called regular reflection.
Regular reflection.
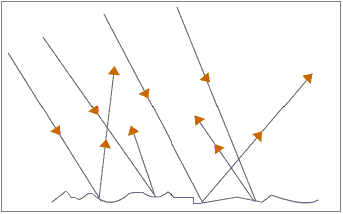
If mirrors were replaced by a piece of sheet of paper, there would be no image to be seen even as a result of diffuse or irregular reflection, this is shown below.
Irregular or diffuse reflection.
Terms used in reflection
When light rays strike a surface (e.g a mirror) there are two rays of importance, namely Incident and Reflected rays, see the figure below:
Reflection of light rays.
- MO is a ray of light falling on a mirror; it is called the incident ray.
- OP is a ray of light leaving the mirror after reflection; it is called the reflected ray. Line NO is perpendicular to the mirror , it is called the normal. ANGLE MON is called the angle of incidence. (i) this is the angle between the incident ray and the normal , angle NOP is called the angle of reflection (t). this is the angle between reflected ray and the normal.
